Brillantgrünsolvolyse

PDF-Version mit Messwertvorlage zum Ausdrucken

Theoretische Grundlagen

Die Reaktionsgeschwindigkeit der Brillantgrünsolvolyse soll in Abhängigkeit des pH-Wertes untersucht und die Geschwindigkeitskonstanten berechnet werden.

Reaktionsgleichung von Brillantgrün mit Hydroxidionen und Wasser.

Kinetik

Das dunkelgrüne Brillantgrün B reagiert unter Zugabe von Wasser oder Hydroxidionen zu seiner Carbinolbase C, die farblos erscheint (Abbildung ). Das Geschwindigkeitsgesetz mit den Geschwindigkeitskonstanten $k_1$ und $k_2$ lautet daher

\frac{\text{d}c_\text B}{\mathrm d t}=-k_1c_\ce{OH^{-}}\,c_\text B - k_2 c_\ce{H_2O}\,c_\text B

Damit handelt es sich um eine Reaktion zweiter Ordnung. Im Folgenden werden sinnvolle Annahmen gemacht, die die Reaktion zweiter Ordnung in eine erster Ordnung überführen.

Die Wasser-Konzentration ist konstant.

Diese Annahme ist sinnvoll, da in wässriger Lösung ein Überschuss an Wassermolekülen vorliegt und sich die Konzentration im Verlauf der Reaktion daher kaum ändert. Die Wasser-Konzentration kann daher in eine neue Geschwindigkeitskonstante einbezogen werden, der Teilgeschwindigkeitskonstanten $k'_2$ .
$k'_2=k_2\,c_\ce{H_2O}$
Die Hydroxidionen-Konzentration ist konstant. Diese Annahme kann gemacht werden, da der pH-Wert der im Versuch verwendeten Lösung durch ein Puffersystem konstant gehalten wird.
$k'_1=k_1\,c_\ce{OH^{-}}$

Mit diesen Annahmen lässt sich Gleichung zu

\frac{\text{d}c_\text B}{\mathrm d t}= -\underbrace{\left(k'_2 + k'_1\right)}_{ = k} c_\text B

vereinfachen. Die Darstellung der Gesamtgeschwindigkeitskonstante $k$ als

k =k'_2 + k_1\,c_\ce{OH^{-}}

erlaubt eine Bestimmung der Teilgeschwindigkeitskonstanten $k'_2$ und $k'_1$ durch die Auftragung der Gesamtgeschwindigkeitskonstanten $k$ gegen die Hydroxidionenkonzentration. Auch wird nun ein Geschwindigkeitsgesetz erster Ordnung erhalten.

\frac{\text{d}c_\text B}{\mathrm d t}=-k c_\text B

Diese Gleichung ist durch Separation der Variablen und anschließender Integration zu lösen.

\ln \left(\frac{c_\text B(t)}{c_\text B(t_0)}\right)=-k(t-t_0)

Dabei beschreibt der Term $c_\text B(t_0)$ die Konzentration von Brillantgrün zum Zeitpunkt $t_0$ . Es ist zweckmäßig, den Zeitpunkt $t_0$ auf den Start der Messung zu legen, also $t_0 = 0$ .

Das Lambert-Beersche Gesetz

Wird monochromatisches Licht mit der Intensität $I_0$ durch eine lichtabsorbierende Substanz geleitet, verlässt es die Substanz mit der geringeren Intensität $I$ . Die differentielle Abnahme der Intensität $-\mathrm dI$ ist in guter Näherung proportional zu der im differentiellen Wegabschnitt $\mathrm d\ell$ vorherrschenden Intensität $I$ . Die Proportionalitätskonstante wird $k'$ genannt.

-\mathrm{d}I = k' \, I \, \mathrm{d} \ell

Durch Separation der Variablen und anschließender Integration erhält man, unter Berücksichtigung der Logarithmengesetze, das Bouguer-Lambertsche Gesetz.

\ln \left(\frac{I_0}{I}\right)=k'\, \ell

Es wird eine neue Konstante $k$ eingeführt um den natürlichen Logarithmus in den dekadischen Logarithmus zu überführen. Der dekadische Logarithmus des Verhältnisses $\frac{I_0}{I}$ wird Extinktion $E$ genannt.

E = \log \left(\frac{I_0}{I}\right)=k\, \ell

Nach dem Beerschen Gesetz ist die Proportionalitätskonstante $k$ proportional zu der Konzentration $c$ .

k=\varepsilon \, c

Dabei ist $\varepsilon$ der molare dekadische Extinktionskoeffizient. Durch Einsetzen von Gleichung in Gleichung erhält man das Lambert-Beersche Gesetz:

E=\log \frac{I_0}{I}=\varepsilon \, c \, \ell

Die so erhaltenen Gesetze gelten unter folgenden Voraussetzungen:

Das Bouguer-Lambertsche Gesetz gilt nur für monochromatisches Licht in einem optisch homogenen Medium.
Das Beersche Gesetz gilt nur für Lösungen, in denen sich keine konzentrationsabhängigen Gleichgewichte einstellen.
Das Lambert-Beersche Gesetz gilt nur für niedrig konzentrierte Lösungen, da nur hier die Wechselwirkungen zwischen den Molekülen vernachlässigbar sind.

Isosbestischer Punkt

Mithilfe einer einfachen Methode kann belegt werden, dass die Konzentrationen von Edukten und Produkten während einer Reaktion in einem festen stöchiometrischen Verhältnis zueinander stehen. Daraus folgt, dass die Reaktion ohne Folge- und Nebenreaktionen stattfindet und die oben dargestellten einfachen Kinetikgesetze gelten . Bei Extinktionsmessungen wird die Extinktion als Funktion der Wellenlänge in einem Spektrum dargestellt. Für die Extinktion einer Reaktion, an der zwei absorbierende Substanzen A und B teilnehmen, gilt

E = \ell(\varepsilon_\text A \, c_\text A + \varepsilon_\text B \, c_\text B)

Die molaren Extinktionskoeffizienten sind wellenlängenabhängige Stoffkonstanten, ihr Verhältnis zueinander lässt sich durch einen Faktor $\nu$ ausdrücken.

\varepsilon_\text A= \nu \, \varepsilon_\text B

Diese Beziehung kann in Gleichung eingesetzt werden, wodurch man folgenden Zusammenhang erhält:

E= \ell\, \varepsilon_\text B \, (\nu \, c_\text A + c_\text B)

Es wird der Fall untersucht, dass $\nu$ das stöchiometrische Verhältnis wiedergibt, da sich dann der Term in den Klammern als Gesamtkonzentration $c_0$ darstellen lässt. Damit sind alle Terme auf der rechten Seite konstant.

E = \ell\, \varepsilon_\text B \underbrace{(\nu \, c_\text A + c_\text B )}_{c_0}= \mathrm{konst}

Das bedeutet, dass die Extinktion an allen Punkten, an denen das Verhältnis der molaren Extinktionskoeffizienten von A und B die Stöchiometrie wiedergibt, konstant ist. Diese Punkte werden isosbestische Punkte genannt. Betrachtet man mehrere zeitlich versetzt aufgenommene Spektren in einem Graphen, so handelt es sich bei der Wellenlänge, bei der sich alle Kurven schneiden, um den isosbestischen Punkt. Wie viele isosbestische Punkte beobachtet werden können liegt unter anderem am Spektrum von Edukt und Produkt.

Extinktionsmessung von Brillantgrün

Brillantgrün besitzt eine Extinktionsbande im sichtbaren Lichtspektrum und erscheint daher grün. Die Carbinolbase hingegen erscheint farblos. Die Konzentrationsabnahme lässt sich daher spektralphotometrisch verfolgen . Da der molare Extinktionskoeffizient $\varepsilon$ für Brillantgrün besonders groß ist, reichen schon geringste Konzentrationen dieser Substanz aus, um Lösungen grün zu färben. Einsetzen des Lambert-Beerschen Gesetzes (Gleichung )

E(t) = \varepsilon\,c_\text B(t)\,\ell \qquad\qquad E(t = t_0) = E_0 = \varepsilon\,c_\text B(t_0)\,\ell

in Gleichung liefert mit $t_0 = 0$ dann unmittelbar

\ln \left(\frac{E(t)}{E_0}\right)=-kt

Dabei ist $E_0$ die Extinktion zum Zeitpunkt $t = 0$ , also dem Start der Messung. Diese Beziehung ermöglicht es die Gesamtgeschwindigkeitskonstante zu ermitteln, indem man $\ln\left(\frac{E}{E_0}\right)$ als Funktion der Messzeit $t$ aufträgt und die Steigung mithilfe eines Fits bestimmt. Dabei gilt Gleichung nur unter der Voraussetzung, dass bei der Wellenlänge, bei der die Extinktion $E$ gemessen wird, ausschließlich der Farbstoff Brillantgrün absorbiert. Um zu prüfen, ob diese Voraussetzung erfüllt ist, müssen die Extinktionsspektren der Reinsubstanzen Brillantgrün und Carbinolbase aufgenommen werden. Während diese Messung im Fall des Brillantgrüns direkt erfolgen kann, kann das Spektrum der Carbinolbase nur indirekt ermittelt werden, weil diese erst im Verlauf der Reaktion gebildet wird. Daher werden mehrere Spektren der Reaktionslösung zeitlich versetzt aufgenommen.

pH-Wert

Der pH-Wert ist der negative dekadische Logarithmus der Konzentration an Oxoniumionen. Definitionsgemäß wird die Konzentration an Oxoniumionen in der Einheit mol / L angegeben.

\mathrm{pH} = -\log{\left(\frac{c_\ce{H_3O^+}}{\pu{mol / L}}\right)}

Der pH-Wert wird mit Hilfe einer Glaselektrode bestimmt. Analog dazu ist der pOH-Wert

\mathrm{pOH} = -\log{\left(\frac{c_\ce{OH^{-}}}{\pu{mol / L}}\right)}

Aus dem Ionenprodukt der Autoprotolysereaktion von Wasser folgt

\mathrm{pH} + \mathrm{pOH} = 14

Versuchsaufbau

In diesem Versuch wird die Kinetik der Brillantgrünsolvolyse in Abhängigkeit von dem pH-Wert bei konstanter Temperatur untersucht. Zur Messung des pH-Wertes wird ein digitales pH-Meter mit Glaselektrode verwendet. Die Konzentrationsänderungen des Brillantgrüns werden durch Messungen der Absorption mit einem Spektralphotometer mit temperierbarem Probenhalter verfolgt.

Spektralphotometer

Im Versuch wird ein handelsübliches Spektralphotometer benutzt. Der Aufbau des Spektralphotometers ist schematisch in Abbildung dargestellt.

Schematischer Aufbau eines Spektrometers.

Die Lichtquelle dient dazu, ein möglichst breites Wellenlängenspektrum zur Verfügung zu stellen. Üblicherweise verwendet man hierzu Wolfram-, Deuterium- oder Xenonlampen, letztere wird im Praktikum eingesetzt. Aufgabe des Monochromators ist es, das einfallende Licht nach der Wellenlänge aufzuteilen (zu monochromatisieren), so dass immer nur Licht eines möglichst engen Spektralbereichs durch die Probe strahlt. Als Monochromatoren verwendet man Prismen oder, wie in diesem Versuch, Gitter. Nach dem Durchstrahlen der Küvette wird die Lichtintensität mit Hilfe von Photomultipliern oder Photodioden in elektrischen Strom umgewandelt und gemessen.

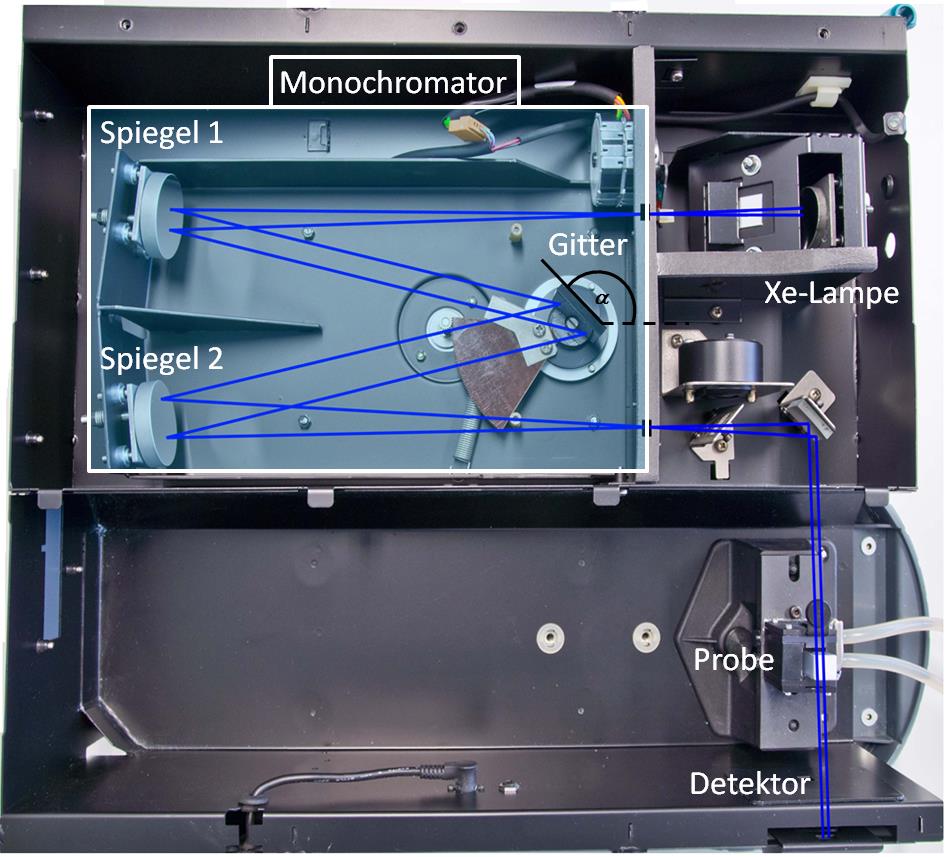
Der Strahlengang des verwendeten Spektralphotometers ist in Abbildung dargestellt.

Die verwendete Küvette besteht aus Quarzglas, da herkömmliches Glas in dem betrachteten Wellenlängenbereich zu stark absorbiert. Um die Messung bei einer kontrollierten Temperatur durchzuführen, befindet sich im Photometer eine Temperierhalterung, in die die Küvette gesteckt wird. Mithilfe eines Thermostaten kann diese Temperatur eingestellt und konstant gehalten werden.

Die Quarzküvette besitzt zwei klare (Strahldurchführung) und zwei mattierte Seitenwände. Für die Messungen im Photometer muss die Küvette stets so in den Küvettenhalter gesetzt werden, dass der Lichtstrahl durch die klaren Seitenwände fällt. Achten Sie darauf, dass sie diese Seiten nie mit den Fingern berühren! Halten Sie die Küvette deshalb stets am obersten Ende der mattierten Seitenwände.

Chemikalien

Folgende Lösungen stehen bereits angesetzt aus:

Wässrige Brillantgrün-Lösung mit einer Konzentration von 0,000104 mol / L.
Vier Pufferlösungen A, B, C und D aus wässriger Borax-Stammlösung (Dinatriumtetraborat $\ce{Na_2B_4O_7}$ , 0,025 mol / L). Die Einstellung des pH-Wertes erfolgte mit wässriger Kaliumhydroxid-Lösung (0,1 mol / L). Verschiedene Ionenstärken verfälschen die Messergebnisse. Mit Hilfe einer wässrigen Kaliumchlorid-Lösung (0,1 mol / L) wurden die Pufferlösungen so eingestellt, dass alle Lösungen die selbe Ionenstärke an Kalium-Ionen besitzen.

Durchführung

Tutorial zur virtuellen Durchführung

Zur virtuellen Versuchsdurchführung (Spektrumaufnahme) Zur virtuellen Versuchsdurchführung (Extinktions-Zeit-Kurven)

Videoanleitung zum Laborversuch

Vorbereitung

Schalten Sie den Computer an und melden Sie sich mit dem Benutzer .\Praktikum und dem Kennwort Passwort* an.
Stellen Sie den Thermostaten auf eine Temperatur von 25 °C ein und drehen Sie das Kühlwasser auf.
Messen Sie die pH-Werte der Pufferlösungen mithilfe des pH-Meters. Die Messung kann zu einem beliebigen Zeitpunkt während der Durchführung erfolgen.

Hinweis beim interaktiven Versuch: Warten Sie etwa 10 Sekunden, bis sich der pH-Wert nach der Auswahl der Lösung auf einen konstanten Wert eingestellt hat. Klicken Sie dann auf Reaktion erneut starten und anschließend auf Neues Spektrum aufzeichnen bzw. Neue Zeitserie aufzeichnen.

Extinktionsspektrum von Brillantgrün

Zur interaktiven Versuchsdurchführung (Spektrumaufnahme)

Nehmen Sie das Extinktionsspektrum von reinem Brillantgrün bei 25 °C im Wellenlängenbereich von 250 nm bis 800 nm auf.

Stellen Sie die Küvette in die Temperiervorrichtung des Photometers und geben Sie mit der Mikropipette ein Volumen von 2,5 mL Wasser in die Küvette.
Die Celsiustemperatur der Küvette mit der Probe wird vom Spektralphotometer automatisch gemessen und angezeigt. Warten Sie, bis dieser über einen Zeitraum von drei Minuten eine konstante Celsiustemperatur von 25 °C hat.
Starten Sie das Programm Spektrum Brillantgrün. Das Programm gibt zwei Meldungen aus, die angeben, dass keine Basislinienkorrektur vorliegt. Bestätigen Sie beide Meldungen mit Ok.
Erstellen Sie zunächst eine Basislinienkorrektur durch Drücken von Baseline. Der Vorgang ist beendet, wenn wieder alle Schaltflächen im Programm verfügbar sind.
Jetzt kann das Spektrum von Brillantgrün gemessen werden. Drücken Sie dazu Start und geben Sie den Speicherort und einen aussagekräftigen Dateinamen für Ihre Messdaten an. Die Dateien sollen im Ordner D:\Userdaten\ als CSV-Datei gespeichert werden. Legen Sie darin einen Ordner mit Ihrer Gruppennummer an. Bestätigen Sie mit Save.
Geben Sie jetzt mit der Mikropipette ein Volumen von 0,3 mL der Brillantgrünlösung zu dem Wasser in die Küvette. Durchmischen Sie die Lösung sorgfältig durch wiederholtes Ansaugen und Ablassen der Mischung mithilfe der Pipette.
Drücken Sie zum Start der Messung im Dialogfenster Sample Name den Knopf Ok. Der Name, der an dieser Stelle angegeben wird, ist unerheblich. Daraufhin erscheint ein Fenster mit ablaufendem zwei-Minuten-Timer. Während dieser Zeit muss erneut Ok gedrückt werden, um die Messung zu beginnen.
Die Messung kann am Monitor verfolgt werden. Währenddessen werden nacheinander fünf Graphen vom Programm erstellt. Beendet ist die Messung sobald Start wieder hellgrau hinterlegt ist.
Wenn die Messung beendet ist, wird im Dialogfenster Sample Name der Knopf Finish gedrückt.
Lesen Sie in dem Diagramm die Wellenlänge des Extinktionsmaximums ab und notieren Sie diese. Für eine genauere Betrachtung des Extinktionsmaximums kann dieses, durch Halten der linken Maustaste und Einrahmung eines Diagrammabschnitts, vergrößert dargestellt werden. Schließen Sie das Programm. Die Werte werden automatisch gespeichert.
Entnehmen Sie die Küvette aus der Temperiervorrichtung und überprüfen Sie sie auf mögliche Verunreinigungen und Lufblasen. Leeren Sie den Inhalt der Küvette in das Abfallgefäß, spülen Sie die Küvette mit vollentsalzenem Wasser aus und trocknen Sie diese mit fusselfreien Tüchern.

Hinweis beim interaktiven Versuch: Die Basislinienkorrektur ist unnötig. Verwenden Sie Puffer A für die Messung des Spektrums.

Extinktions-Zeit-Kurven

Zur interaktiven Versuchsdurchführung (Extinktions-Zeit-Kurven)

Messen Sie die Extinktion bei der Wellenlänge des Extinktionsmaximums von Brillantgrün für jeden der vier pH-Werte bei 25 °C über einen Zeitraum von jeweils 4 Minuten.

Befüllen Sie die Küvette mit 2,5 mL der Pufferlösung A und stellen Sie diese in die Temperiervorrichtung des Photometers.
Messen Sie die Temperatur der befüllten Küvette. Warten Sie, bis der Inhalt der Küvette über einen Zeitraum von drei Minuten eine konstante Temperatur von 25 °C hat.
Öffnen Sie das Programm Extinktions-Zeit-Kurven.
Stellen Sie über die Schaltfläche Setup die Wellenlänge des Extinktionsmaximums von Brillantgrün ein und übernehmen Sie die Einstellung mit Ok.
Drücken Sie Start und geben Sie den Speicherort und einen aussagekräftigen Dateinamen für Ihre Messdaten an (aus technischen Gründen können zur Benennung nur Buchstaben und Zahlen verwendet werden). Die Dateien sollen im Ordner D:\Userdaten\Gruppennummer gespeichert werden. Bestätigen Sie mit Save.
Geben Sie jetzt mit der Mikropipette ein Volumen von 0,3 mL der Brillantgrünlösung zu der Pufferlösung in die Küvette. Durchmischen Sie die Lösung sorgfältig durch wiederholtes Ansaugen und Ablassen der Mischung mithilfe der Pipette.
Drücken Sie zum Start der Messung im Dialogfenster Loading Guide den Knopf Ok. Der Name, der an dieser Stelle angegeben wird, ist unerheblich. Drücken Sie auch im nächsten erscheinenden Dialogfenster Sync Start auf Ok.
Die Messung kann am Monitor verfolgt werden. Dabei ist es sinnvoll, über das Doppelpfeilsymbol oder durch Scrollen eine sinnvolle Skalierung der Achsen einzustellen.
Entnehmen Sie die Küvette aus der Temperiervorrichtung und überprüfen Sie sie auf mögliche Verunreinigungen und Lufblasen. Leeren Sie den Inhalt der Küvette nach dem Ende der Messung in das Abfallgefäß, spülen Sie die Küvette mit vollentsalzenem Wasser aus und trocknen Sie diese mit fusselfreien Tüchern.

Wiederholen Sie die Messung für Puffer B bis D. Ein erneuter Programmstart ist nicht erforderlich.

Zeitversetzte Spektren

Zur interaktiven Versuchsdurchführung (Spektrumaufnahme)

Bei einer Temperatur von 25 °C sollen fünf Spektren im Wellenlängenbereich von 250 nm nm bis 800 nm aufgenommen werden. Dabei sollen die Messungen zeitlich um je drei Minuten versetzt erfolgen. Verwenden Sie Pufferlösung D.

Befüllen Sie die Küvette mit 2,5 mL der Pufferlösung D und stellen Sie diese in die Temperiervorrichtung des Photometers.
Messen Sie die Temperatur der befüllten Küvette. Warten Sie, bis der Inhalt der Küvette über einen Zeitraum von drei Minuten eine konstante Temperatur von 25 °C hat.
Öffnen Sie das Programm zeitabhängige Spektren. Das Programm gibt zwei Meldungen aus, die angeben, dass keine Basislinienkorrektur vorliegt. Bestätigen Sie beide Meldungen mit Ok.
Erstellen Sie zunächst eine Basislinienkorrektur durch Drücken von Baseline. Der Vorgang ist beendet, wenn wieder alle Schaltflächen im Programm verfügbar sind.
Drücken Sie zum Messen der Spektren Start und geben Sie den Speicherort und einen aussagekräftigen Dateinamen für Ihre Messdaten an (aus technischen Gründen können zur Benennung nur Buchstaben und Zahlen verwendet werden). Die Dateien sollen im Ordner D:\Userdaten\Gruppennummer gespeichert werden. Bestätigen Sie mit Save.
Geben Sie jetzt mit der Mikropipette ein Volumen von 0,3 mL der Brillantgrünlösung zu der Pufferlösung in die Küvette. Durchmischen Sie die Lösung sorgfältig durch wiederholtes Ansaugen und Ablassen der Mischung mithilfe der Pipette.
Drücken Sie zum Start der Messung im Dialogfenster Sample Name den Knopf Ok. Der Name, der an dieser Stelle angegeben wird, ist unerheblich. Drücken Sie auch im nächsten erscheinenden Dialogfenster Sync Start auf Ok.
Das Programm nimmt nun über einen Zeitraum von zwölf Minuten im Abstand von drei Minuten jeweils ein Spektrum auf. Die Messungen können am Monitor verfolgt werden.
Entnehmen Sie die Küvette aus der Temperiervorrichtung und überprüfen Sie sie auf mögliche Verunreinigungen und Lufblasen. Leeren Sie den Inhalt der Küvette nach dem Ende der Messung in das Abfallgefäß, spülen Sie die Küvette mit vollentsalzenem Wasser aus und trocknen Sie diese mit fusselfreien Tüchern.
Nach dem Schließen des Programmes sind die Werte automatisch gespeichert.

Versuchsende

Entsorgen Sie die restlichen Pufferlösungen in die Brillantgrün-Abfallflasche.
Kopieren Sie die CSV-Dateien Ihrer Messungen auf Ihren USB-Stick. Die Original-Daten bleiben auf dem Computer und werden nicht gelöscht.
Schalten Sie das pH-Meter, den Computer, den Thermostaten und das Kühlwasser aus.

Auswertung

Hinweis: Geben Sie bitte alle Messwerte (einschließlich Spektren) im Protokoll an.

Tragen Sie die Extinktion $E$ in Abhängigkeit der Wellenlänge $\lambda$ von Brillantgrün auf. Geben Sie die Wellenlänge $\lambda_\text{max}$ an, bei der Brillantgrün maximal absorbiert. Bestimmen Sie den Fehler von $\lambda_\text{max}$ unter Berücksichtigung der Genauigkeit Ihrer Messung.
Tragen Sie gemäß Gleichung den Term $\ln \left(\frac{E}{E_0}\right)$ gegen die Zeit in min auf. Fassen Sie die Verläufe der verschiedenen pH-Werte in einem Diagramm zusammen. Berücksichtigen Sie die signifikanten Stellen der Extinktionswerte. Bestimmen Sie aus den Geradensteigungen die Geschwindigkeitskonstanten $k$ sowie deren Fehler. Wählen Sie jeweils einen sinnvollen Bereich für die lineare Regression aus. Diskutieren Sie den Einfluss des pH-Wertes auf die Gesamtgeschwindigkeitskonstante $k$ .
Tragen Sie die Extinktion $E$ in Abhängigkeit der Wellenlänge $\lambda$ der zeitlich versetzt aufgenommenen Spektren von Brillantgrün in einem Diagramm auf. Diskutieren Sie den Verlauf und geben Sie die Wellenlängen der isosbestischen Punkte sowie deren Fehler an.
Tragen Sie gemäß Gleichung die Gesamtgeschwindigkeitskonstanten $k$ in Abhängigkeit der Hydroxidionenkonzentration $c_\ce{OH^{-}}$ auf. Bestimmen Sie daraus die Geschwindigkeitskonstanten der Teilreaktionen $k'_1$ und $k'_2$ sowie deren Fehler. Vergleichen Sie die Geschwindigkeiten der Teilreaktionen bei verschiedenen pH-Werten. Überprüfen Sie, ob Sie die folgenden theoretischen Werte der Geschwindigkeitskonstante $k'_1$ reproduzieren konnten :
$\begin{aligned} \text{pH} = \text{10,3} \pm \text{0,1} :\quad k'_1~&= \pu{(0,0025+-0,0005) / min}\\ \text{pH} = \text{10,6} \pm \text{0,1} :\quad k'_1~&= \pu{(0,0050+-0,0005) / min}\\ \text{pH} = \text{11,0} \pm \text{0,1} :\quad k'_1~&= \pu{(0,015+-0,005) / min}\\ \text{pH} = \text{11,6} \pm \text{0,1} :\quad k'_1~&= \pu{(0,049+-0,005) / min} \end{aligned}$

Vorbereitung auf das Kolloquium

Das Kolloquium beinhaltet zwei Themen. In beiden Themen wird vorausgesetzt, dass von den besprochenen Größen die physikalische Bedeutung, die Einheit und die Berechnung des zugehörigen Fehlers bekannt sind.

Erstes Thema:

Erläutern Sie Versuchsziele, Versuchsdurchführung, verwendete Apparaturen und gemessene Größen.

Zweites Thema:

Erläutern Sie die Bedeutung der Gesamtgeschwindigkeitskonstante $k$ und der Teilgeschwindigkeitskonstanten $k'_1$ und $k'_2$ und zeigen Sie wie sie bestimmt werden.

Theoretische Grundlagen