Physical Chemistry Lab Course

Brilliant green solvolysis

German version

Theory

The reaction speed of the brilliant green solvolysis is investigated as function of pH and the reaction speed constant is determined.

Brilliant green solvolysis

Reaction equation
Reaction equation of the solvolysis of brilliant green (left) with hydroxide ions and water to the carbinol base (right).

Kinetics

The dark green compound brilliant green (B) reacts with water or hydroxide ions to the carbinol base (C) which appears colorless (figure ). The reaction kinetics can be described using the reaction speed constants k_1 and k_2 as

\frac{\text{d}c_\text B}{\mathrm d t}=-k_1c_\ce{OH^{-}}\,c_\text B - k_2 c_\ce{H_2O}\,c_\text B

Thus, the reaction kinetics are of second order. By using two approximations we simplify the kinetics to a first-order equation:

With these approximations, equation is simplified to

\frac{\text{d}c_\text B}{\mathrm d t}= -\underbrace{\left(k'_2 + k'_1\right)}_{ = k} c_\text B.

The decomposition of the reaction speed constant k as

k =k'_2 + k_1\,c_\ce{OH^{-}}

allows to determine the quantities k'_2 and k'_1 by plotting the total reaction speed constant k against the concentration of hydroxide ions. Now, the reaction kinetics are of first order.

\frac{\text{d}c_\text B}{\mathrm d t}=-k c_\text B

The equation can be solved by separation of the variables and subsequent integration.

\ln \left(\frac{c_\text B(t)}{c_\text B(t_0)}\right)=-k(t-t_0)

The term c_\text B(t_0) describes the concentration of brilliant green at time t_0. It is useful to consider the time t_0 as the start of the measurement, thus t_0 = 0.

Lambert-Beer law

If monochromatic light with intensity I_0 travels through a light-absorbing substance, the intensity of the outgoing light I is reduced. The differential reduction of the intensity -\mathrm dI is in good approximation proportional to the intensity I within the differential travel distance \mathrm d\ell. The proportionality constant is called k'.

-\mathrm{d}I = k' \, I \, \mathrm{d} \ell

Using separation of variables and subsequent integration results in the Bouguer-Lamber law.

\ln \left(\frac{I_0}{I}\right)=k'\, \ell

A new constant k is introduced to convert from the natural logarithm to the decadic logarithm. The decadic logarithm of the ratio \frac{I_0}{I} is called extinction E.

E = \log \left(\frac{I_0}{I}\right)=k\, \ell

According to the Beer law the proportionality constant k is proportional to the concentration c.

k=\varepsilon \, c

Here, \varepsilon is the molar decadic extinction coefficient. Inserting equation in equation yields the Lambert-Beer law:

E=\log \frac{I_0}{I}=\varepsilon \, c \, \ell

The following prerequisites are required for the Lambert-Beer law to be valid:

Isosbestic point

A simple method allows to check whether the concentration of reaction educts and products is described using a fixed stoichiometric ratio. This allows to confirm whether the reaction takes places without additional follow-up or side reactions . The extinction can be measured as a function of wavelength, resulting in a spectrum. In case of a reaction, in which two absorbing compounds A and B take part, the extinction is

E = \ell(\varepsilon_\text A \, c_\text A + \varepsilon_\text B \, c_\text B).

The molar extinction coefficients are wavelength-dependent properties. Their ratio can be described using a factor \nu.

\varepsilon_\text A= \nu \, \varepsilon_\text B

Using this relationship in equation yields:

E= \ell\, \varepsilon_\text B \, (\nu \, c_\text A + c_\text B)

We now focus on the case that \nu is the stoichiometric ratio, since the term in parenthesis is the total concentration c_0. Then the right-hand side of the equation consists only of constants.

E = \ell\, \varepsilon_\text B \underbrace{(\nu \, c_\text A + c_\text B )}_{c_0}= \mathrm{const}

This means, that the extinction is constant for all wavelengths at which the ratio of the molar extinction coefficients equals the stoichiometric ratio. These points are called isosbestic points. If multiple spectra taken at different times during a reaction exhibit points at which the extinction is constant at one or more particular wavelengths, these points are called isosbestic points. The number of isosbestic points that can be observed depends, among others, on the spectrum of educt and product compounds.

Extinction measurements of brilliant green solutions

Brilliant green absorbs light in the visible spectrum and appears green. In contrast, the carbinol base appears colorless. The reduction of brilliant green concentration as a function of time can thus be followed using a spectral photometer . Since the molar extinction coefficient of brilliant green \varepsilon is rather larger, even small amounts of the substance result in greenly-colored solutions. Using the Lambert-Beer law (equation )

E(t) = \varepsilon\,c_\text B(t)\,\ell \qquad\qquad E(t = t_0) = E_0 = \varepsilon\,c_\text B(t_0)\,\ell

in equation yields with t_0 = 0 the equation

\ln \left(\frac{E(t)}{E_0}\right)=-kt.

Here, E_0 is the extinction at time t = 0 (i.e. at the start of the measurement). This relationship allows to determine the reaction speed constant be plotting \ln\left(\frac{E}{E_0}\right) as function of the measuring time t and determining the slope using a linear fit. It is important to note that equation only holds if the extinction E is measured at a wavelength at which only brilliant green absorbs light. In order to check for this prerequisite, the individual spectra of the pure substances brilliant green and the carbinol base have to be recorded. While this measurement is straight forward for the case of brilliant green, the spectrum of the carbinol base can be only obtained indirectly, as it is produced during the reaction. For this reason, multiple spectra are recorded at different time offsets.

pH value

The pH of a solution is the negative decadic logarithm of the concentration of oxonium ions. Per definition, the concentration of oxonium ions is expressed in units of mol / L.

\mathrm{pH} = -\log{\left(\frac{c_\ce{H_3O^+}}{\pu{mol / L}}\right)}

The pH can be determined using a glass electrode. Analogously, the pOH value is defined as

\mathrm{pOH} = -\log{\left(\frac{c_\ce{OH^{-}}}{\pu{mol / L}}\right)}.

From the ionic product of the autoprotolysis reaction of water follows that

\mathrm{pH} + \mathrm{pOH} = 14

Experimental setup

In this lab course the kinetics of the brilliant green solvolysis is investigated as function of pH at constant temperature. The pH is measured with a digital pH meter with a glass electrode. The concentration change in the solution is determined by measuring the absorption using a spectral photometer with a temperature-controlled sample holder.

Spectral photometer

A commercial spectral photometer is used. The setup is schematically shown in figure .

Schematic setup of the spectral photometer
Schematic setup of the spectral photometer.

The purpose of the light source is to provide a broad spectrum of light. Typically, tungstic, deuterium or xenon lamps are used (the latter is used in the lab course). The monochromator (a prism or diffraction grating) splits the incoming light according to the wave length, such that light from a narrow part of the spectrum reaches the sample. In this lab course, a diffraction grating is used. After passing through the sample, the light intensity is converted into an electric signal by using photo multipliers or photo diodes.

The optical beam bath is shown in figure .

The used cuvette is made from fused silica, since normal glass would absorb light in the used wavelength range. To perform the measurement at a fixed, controlled temperature, the sample holder is placed in a temperature-controlled surrounding. A thermostat is used to adjust the temperature.

The cuvette has two matt and two optically clear sides for passing through the beam. Make sure that the clear sides are used for the light beam and do not touch these sides with your hand. Use the matt sides to hold the cuvette with your hands.

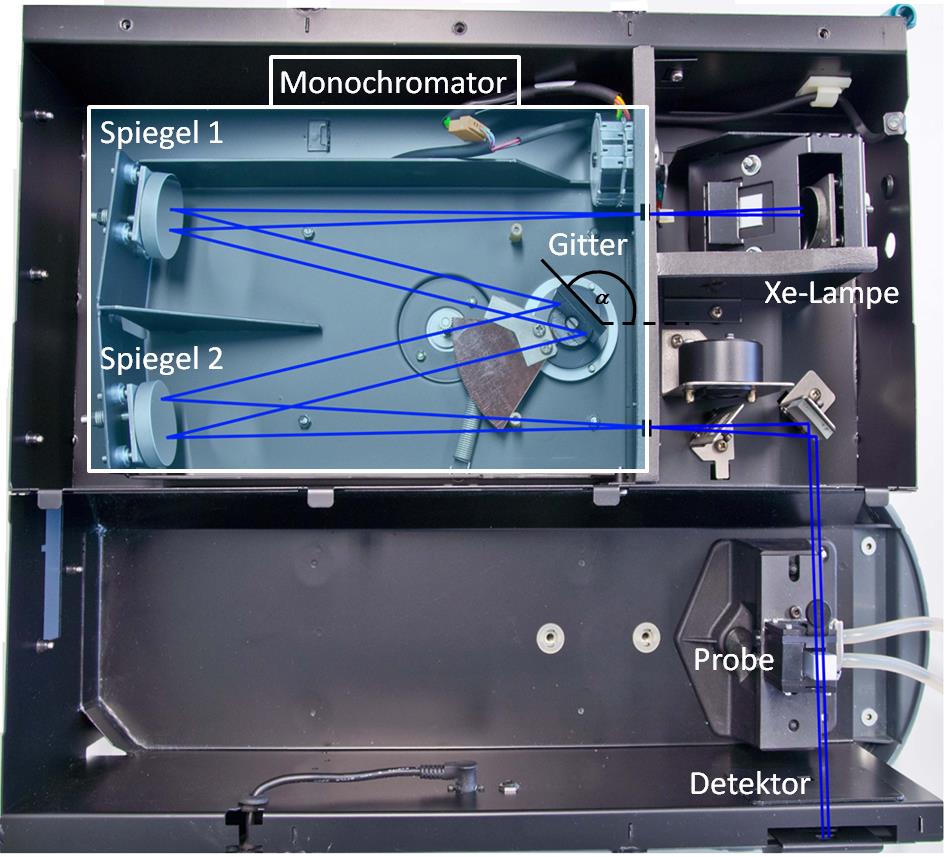
Optical beam path of the used spectral photometer
Optical beam path of the used spectral photometer. (Spiegel means mirror, Gitter means grating, Lampe means lamp, Probe means sample).

Chemicals

The following stock solutions are provided:

Instructions

Virtual lab course video tutorial

Go to virtual lab course (Part 1, recording spectra) Go to virtual lab course (Part 2, time-dependent measurements)

Lab course instructions

Preparation

Notes for the interactive experiment Wait about 10 seconds until the pH value has reached a constant value after selecting the solution. Then click on Restart reaction and then on Record new spectrum or Record new time series.

Extinction spectrum of brilliant green

Go to virtual lab course (Part 1, recording spectra)

Record an extinction spectrum of brilliant green at 25 °C in a wavelength range between 250 nm to 800 nm.

Notes for the interactive experiment The baseline correction is unnecessary. Use buffer A to measure the spectrum.

Time-dependent extinction curves

Go to virtual lab course (Part 2, time-dependent measurements)

Measure the extinction at the wavelength where the extinction was at a maximum for each of the four buffer solutions at 25 °C for a time span of four minutes each.

Repeat the measurement with buffer solutions B, C, and D.

Spectra at different time offset

Go to virtual lab course (Part 1, recording spectra)

Record five spectra in the wavelength range of 250 nm to 800 nm at 25 °C. Each measurement should be offset from the other by three minutes. Use buffer solution D.

End of experiment

Analysis

Note: State all measured raw data values (including spectra) in your report.

Bibliography