Erinnern Sie sich zunächst daran, dass die Berechnung eines Integrals nichts anderes ist als die Ermittlung einer Fläche.
Es gibt verschiedene Methoden der numerischen Integration. Hier wird uns die Trapezformel beschäftigen.
Trapezformel
Angenommen, wir möchten \[ \int_{0}^{3} f(x) \mathrm{d} x \] \[ f(x) = x^3 - 5 x^2 + 7 x + 1 \] finden. Dies entspricht der Fläche des in der nachstehenden Abbildung hellblau schattierte Bereichs.
Das Intervall wird dann in kleinere Intervalle unterteilt, von denen jedes durch ein Trapez angenähert wird. (Man kann es auch als Annäherung einer Kurve durch Linien sehen.) In wie viele Intervalle die Kurve unterteilen wird, hängt davon ab, welche Genauigkeit Sie erreichen möchten (aber darauf gehen wir hier nicht ein).
Sie können mit dem Schieberegler der Anzahl der Unterteilungen $n$ unten spielen. Wenn Sie $n = 3, 4, 5$ betrachten, können Sie sehen, was wir jetzt machen möchten. Und Sie werden sehen, dass die Fläche dem gewünschten Bereich immer näher kommen, wenn Sie $n$ immer weiter erhöhen.
| $S$ | $9.75$ |
|---|---|
| $S'$ | |
| Error $/ \%$ |
Dabei ist $S$ der wahre Wert, $S'$ der Wert, der sich aus der Trapezformel ergibt, und Error ist $(S' - S) / S$ (ausgedrückt in Prozent).
Die Trapezformel zeichnet sich dadurch aus, dass
-
jedes Intervall nicht konstant sein muss.
Wenn die Intervalle konstant sind
Die Symbole werden wie in der folgenden Abbildung gezeigt definiert.
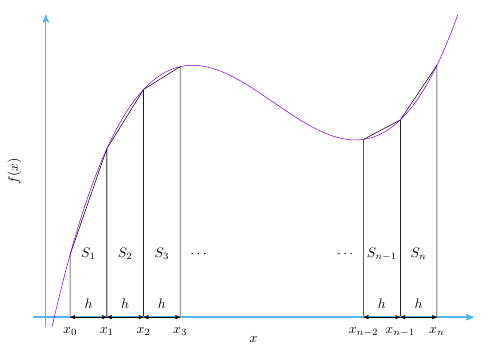
Konzept
Beginnen wir mit dem einfachsten Fall, also bei dem die Intervalle konstant sind. Sei $h$ die Länge der einzelnen Intervalle.
Dann:
-
Die Fläche $S_1$ des ersten Trapezes ist: $$ S_1 = \frac{\left(f(x_0) + f(x_1)\right) h}{2} $$
-
Die Fläche $S_2$ des zweiten Trapezes ist: $$ S_2 = \frac{\left(f(x_1) + f(x_2)\right) h}{2} $$
-
…
-
Die Fläche $S_n$ des letzten Trapezes ist: $$ S_n = \frac{\left(f(x_{n-1}) + f(x_n)\right) h}{2} $$
Alles was bleibt ist diese zu addieren. Mit anderen Worten, der genährte Wert des gesuchten Integrals $S'$ lautet wie folgt:
$$\begin{align*} S' & = \frac{\left(f(x_0) + f(x_1)\right) h}{2} + \frac{\left(f(x_1) + f(x_2)\right) h}{2} + \cdots + \frac{\left(f(x_{n-1}) + f(x_n)\right) h}{2} \quad . \end{align*}$$
Jetzt können wir das als Programm schreiben.
Vereinfachung
Aber warten Sie einen Moment! Denken wir mal darüber nach.
Zunächst einmal:
Betrachten wir also die obige Gleichung nochmal.
-
Betrachten Sie $S_1$ und $S_2$ genau. Beide enthalten $\frac{f(x_1) h}{2}$. Wir brauchen gar nicht erst durch 2 zu dividieren, da wir zwei halbierte Werte addieren.
-
In ähnlicher Weise wird $f(x_1)$ zweimal berechnet, was aber nur einmal geschehen kann.
-
Außerdem gilt für alle $S_i \; (i = 1, 2, ..., n)$, dass sie mit $h$ multipliziert werden, aber wir brauchen sie nicht jedes Mal zu multiplizieren, sondern nur einmal am Ende.
Im Allgemeinen ist die Berechnung von $f(x)$ sehr zeitaufwendig. (In den meisten Fällen, in denen sie nicht zeitaufwendig ist, kann sie ohne numerische Integration durchgeführt werden.) Wenn zum Beispiel $f(x) = \mathrm{e}^{-x^2}$, dann dauert die Berechnung von $x^2$ Zeit, und die Berechnung von $\exp$ dauert noch länger. Daher sollte auch die Anzahl der Berechnungen von $f(x)$ so weit wie möglich reduziert werden.
Letztendlich kann die obige Gleichung wie folgt umgeschrieben werden: \[ S' = \left( \frac{f(x_0)}{2} + f(x_1) + f(x_2) + ... + f(x_{n-1}) + \frac{f(x_n)}{2} \right) h \] oder, wenn wir etwas genauer sind: \[ S' = \left( \frac{f(x_0) + f(x_n)}{2} + f(x_1) + f(x_2) + ... + f(x_{n-1}) \right) h \]
Die Anzahl der Multiplikationen ist von $n$ mal auf 1 (!) gesunken. Die Anzahl der Divisionen wurde ebenfalls von $n$ auf 2 oder 1 reduziert. Außerdem kommt $f(x)$ in der ersten Gleichung $2n$ mal vor, in der zweiten Gleichung aber nur $n + 1$ mal, also fast die Hälfte. Diese sind mathematisch identisch, aber wenn man sie sich als Computerberechnungen vorstellt, sind sie unterschiedlich.
Teilzusammenfassung
Die Vorgehensweise beim Schreiben eines Programms einer Berechnung (nicht nur eines Integrals) ist im Allgemeinen wie folgt.
-
über das Prinzip der Berechnungsmethode nachdenken
-
der notwendigen Formel für die Berechnung herleiten
-
die Formel prüfen und überlegen, ob sie vereinfacht werden kann
-
(endlich) das Programm schreiben
Daraus kann man ersehen, dass die Vorbereitung viel wichtiger ist als das Schreiben des Programms. Wenn Sie die Vorbereitungen vor dem Schreiben des Programms nicht richtig durchführen, kann es passieren, dass das Programm nur sehr langsam berechnet und / oder die Fehlerquote der Ergebnisse hoch wird.
Natürlich ist es keine schlechte Idee, vor allem am Anfang, ein Programm zu schreiben, ohne zu viel nachzudenken. (Viel zu schreiben und dabei auch Fehler zu machen, ist eine gute Erfahrung!) Es ist jedoch wichtig, sich darüber im Klaren zu sein, dass Sie Ihr Programm zu einem späteren Zeitpunkt möglicherweise nochmal überdenken und erheblich ändern müssen.
Wenn das Intervall nicht konstant ist
Die Idee ist fast dieselbe wie für den konstanten Fall, nur dass $h$ durch jedes Intervall $h_1 = x_1 - x_0$, … ersetzt wird.
$$\begin{align*} S' = & \frac{\left(f(x_0) + f(x_1)\right) h_1}{2} + \frac{\left(f(x_1) + f(x_2)\right) h_2}{2} + \cdots + \frac{\left(f(x_{n-1}) + f(x_n)\right) h_{n}}{2} \end{align*}$$
Leider lässt sich die Gleichung in diesem Fall nicht viel vereinfachen.
$$\begin{align*} S' = & \frac{1}{2}\left( f(x_0) h_1 + f(x_1) (h_1 + h_2) + \cdots + f(x_{n-1}) (h_{n-1} + h_{n}) + f(x_n) h_{n} \right) \\ = & \frac{1}{2}\left( f(x_0) (x_1 - x_0) + f(x_1) (x_2 - x_0) + \cdots + f(x_{n-1}) (x_{n} - x_{n-2}) + f(x_n) (x_n - x_{n-1}) \right) \end{align*}$$
Andere Methoden als die Trapezformel
Eine der beliebtesten Methoden der numerischen Integration neben der Trapezformel ist die summierte (zusammengesetzte) Simpsonregel (eng. Composite Simpson's rule). Wenn Sie daran interessiert sind, recherchieren Sie dazu mit Büchern über numerische Berechnungen (oder im Internet).
Übungen (1)
Nun wollen wir ein Programm für die numerische Integration durch Trapezformeln schreiben. Versuchen wir zunächst, den Fläche von $f(x) = x$ zu bestimmen.
-
Zeichnen Sie den Graphen von $f(x) = x$ (auf Papier).
-
Schreiben Sie eine Funktion (in Python) zur Berechnung von $f(x) = x$ und lassen Sie die Werte bei $x = 0, 1$ und $2$ anzeigen. Überprüfen Sie, ob die angezeigten Werte korrekt sind.
Konkret sollte sie ungefähr wie folgt aussehen (Sie können den Namen der Funktion bzw. des Arguments ändern.):
def f(x): # Schreiben Sie hier. return ... print(f(0)) print(f(1)) print(f(2)) -
Berechnen Sie (mit Papier und Bleistift) die folgenden Werte.
$$\begin{align} \int_0^1 f(x) \,\mathrm{d}x \\ \int_1^2 f(x) \,\mathrm{d}x \end{align}$$
-
Schreiben Sie eine Funktion zur Berechnung der numerischen Integration. Die Funktion sollte als Argumente die Untergrenze des Integralintervalls $x_\mathrm{l}$, die Obergrenze des Integralintervalls $x_\mathrm{u}$ und die Anzahl der Teilungen $n$ nehmen. Zum Beipiel:
def integral(xl, xu, n): # Schreiben Sie hier. return ...Sie können den Namen der Funktion sowie der Variablen und/oder die Reihenfolge der Argumente ändern.
Es kann sein, dass Sie beim Schreiben Ihres Programms Schwierigkeiten haben, aber probieren Sie zunächst verschiedene Dinge aus. Ein Hinweis wird anschließend gegeben, aber probieren Sie es aus, ohne vorher nachzusehen. -
Führen Sie die von Ihnen geschriebene Funktion mit den folgenden Wertekombinationen aus. In diesen Fällen sollten Sie jeweils ein absolut korrektes Ergebnis erhalten. (Warum? Überlegen Sie es sich.) Überprüfen Sie, ob Sie die richtigen Ergebnisse erhalten.
-
$(x_\mathrm{l}, x_\mathrm{u}, n) = (0, 1, 1)$
-
$(x_\mathrm{l}, x_\mathrm{u}, n) = (0, 1, 2)$
-
$(x_\mathrm{l}, x_\mathrm{u}, n) = (0, 1, 16)$
-
$(x_\mathrm{l}, x_\mathrm{u}, n) = (0, 1, 1000)$
-
$(x_\mathrm{l}, x_\mathrm{u}, n) = (1, 2, 1)$
-
$(x_\mathrm{l}, x_\mathrm{u}, n) = (1, 2, 2)$
-
$(x_\mathrm{l}, x_\mathrm{u}, n) = (1, 2, 16)$
-
$(x_\mathrm{l}, x_\mathrm{u}, n) = (1, 2, 1000)$
(d. h. numerische Integrationen über die Integralintervalle [0, 1] und [1, 2] in Kombination mit der Anzahl der Teilungen 1, 2, 16 und 1000)
-
Hinweis: Berechnung von $x_i$
Möglicherweise hatten Sie Schwierigkeiten, $x_i$ zu finden.
Methode 1
Der einfachste Weg ist, zunächst $h$ zu finden und es dann zu $x_0$ ($= x_\mathrm{l}$) zu addieren.
x = xl
h = (xu - xl) / n
for i in range(...):
...
x += h
...Der Wert von $h$ kann jedoch Fehler enthalten (innerhalb des Computers), so dass sich bei dieser Methode Fehler ansammeln können. (Siehe auch Worauf ist bei numerischen Berechnungen zu achten: Einführung in Fehler.)
Methode 2
Eine andere Methode ist, jedes Mal $x_i$ zu berechnen, als $$x_i = x_\mathrm{l} + \frac{\left(x_\mathrm{u} - x_\mathrm{l}\right) \times i}{n} \; .$$ Diese kann Fehler unterdrücken, die durch Fehler in $h$ verursacht werden, aber sie erhöht die Anzahl der Multiplikationen und Divisionen.
Vergleich
Vergleichen wir diese Methoden im Hinblick auf die Fehler. Sie fragen sich vielleicht, warum es (manchmal) einen Unterschied gibt, obwohl beide Methoden mathematisch identische Werte liefern sollten. Kurz gesagt, liegt es daran, dass Computer nicht mit unendlichen Ziffern umgehen können.
Der Klarheit halber denken wir in Dezimalzahlen. Angenommen, wir möchten das Intervall [0, 1] in drei Teile unterteilen und den Punkt dazwischen finden. Nehmen wir auch an, dass die signifikanten Stellen drei sind.
Nach der ersten Methode ist $h = (1 - 0) / 3 = 1 / 3 = 0.333$. $x_i$ wird also wie folgt berechnet. $$\begin{align*} x_0 &= 0 \\ x_1 &= x_0 + h = 0.333 \\ x_2 &= x_1 + h = 0.666 \\ x_3 &= x_2 + h = 0.999 \end{align*}$$ Es sollte $x_3 = 1$ sein, aber es gibt einen Fehler aufgrund eines Fehlers in $h$.
Bei der zweiten Methode erfolgt die Berechnung wie folgt. $$\begin{align*} x_0 &= 0 \\ x_1 &= x_0 + \frac{(1 - 0) \times 1}{3} = 0.333 \\ x_2 &= x_0 + \frac{(1 - 0) \times 2}{3} = 0.667 \\ x_3 &= x_0 + \frac{(1 - 0) \times 3}{3} = 1 \end{align*}$$ Es ist zu erkennen, dass der Fehler geringer ist als bei der ersten Methode. (Beachte Sie, dass auch bei der zweiten Methode $x_1$ und $x_2$ keine exakten Werte sind. Sie sind in der Tat Infinitesimale.)
Es ist jedoch zu beachten, dass die erste Methode nicht immer zu einem Fehler führt. Wenn $h$ keinen Fehler enthält (z. B. $h = 0.2$ bei Dezimalsystemen), wird dadurch kein Fehler eingeführt.
-
Zeichnen Sie den Graphen von $f(x) = x^2$.
-
Berechnen Sie (mit Papier und Bleistift) die folgenden Werte.
$$\begin{align} \int_0^1 f(x) \,\mathrm{d}x \\ \int_1^2 f(x) \,\mathrm{d}x \end{align}$$
-
Ändern Sie nur den Teil
f(x)des in der vorherigen Übung erstellten Programms und führen Sie es aus. Überprüfen Sie, welche Werte ermittelt wurden und warum. -
(fakultativ) Wenn Sie Zeit/Lust haben, schreiben Sie Programme für jede der beiden oben genannten Methoden, um $x_i$ zu finden, und vergleichen Sie die Ergebnisse.
Überprüfen der Ergebnisse (1)
Das Korrigieren von Fehlern in einem Programm ist eine schwierigere
Aufgabe als das Schreiben des Programms.
Vor allem bei großen Programmen ist es umso schwieriger, Fehler zu
finden, je später sie auftreten.
Deshalb ist es wichtig, Fehler frühzeitig und gründlich zu beseitigen,
indem man mögliche Fehlerquellen im Voraus erkennt und prüft, ob sie
nicht vorhanden sind.
Leider ist oft Erfahrung erforderlich, um solche
wahrscheinlichen Fehlerstellen
zu erkennen.
(Programmierer, die schon viele Fehler gemacht haben, sind eher in der
Lage, diese Intuition zu nutzen.
Viele Fehler zu machen ist eine Erfahrung wert, besonders wenn man
gerade erst anfängt zu lernen.)
Schauen wir uns einige typische Fehlerpunkte an.
Im Allgemeinen treten Fehler vor allem in Ausnahme-
oder
Sonderfällen
auf, so dass es wichtig ist, zu prüfen, ob das
Programm an solchen Stellen korrekt funktioniert.
In der ersten Übung sollten Sie für $f(x) = x$ mit den folgenden Werten überprüfen.
-
$(x_\mathrm{l}, x_\mathrm{u}, n) = (0, 1, 1)$
-
$(x_\mathrm{l}, x_\mathrm{u}, n) = (0, 1, 2)$
-
$(x_\mathrm{l}, x_\mathrm{u}, n) = (0, 1, 16)$
-
$(x_\mathrm{l}, x_\mathrm{u}, n) = (0, 1, 1000)$
-
$(x_\mathrm{l}, x_\mathrm{u}, n) = (1, 2, 1)$
-
$(x_\mathrm{l}, x_\mathrm{u}, n) = (1, 2, 2)$
-
$(x_\mathrm{l}, x_\mathrm{u}, n) = (1, 2, 16)$
-
$(x_\mathrm{l}, x_\mathrm{u}, n) = (1, 2, 1000)$
Es gibt einen vernünftigen Grund, warum diese Werte gewählt wurden. Zunächst wurde die Funktion $f(x) = x$ gewählt, weil sie leicht zu berechnen ist. Als erstes Integrationsintervall wurde das Intervall [0, 1] gewählt, auch weil es leicht zu berechnen ist. Werden hier falsche Ergebnisse ermittelt, ist es sehr wahrscheinlich, dass das Programm grundlegend falsch ist. Zusätzlich wurden [1, 2] gewählt, um zu überprüfen, dass $x_\mathrm{l}$ korrekt behandelt wird. Beide haben eine Intervalllänge von 1, aber es ist noch besser, zu prüfen, ob es auch anders geht (z. B. die Intervalle [1, 3] und/oder [1, 2.1]).
Für die Anzahl der Teilungen wurde zunächst der Fall $n = 1$ untersucht. Dies hängt davon ab, welches Programm Sie geschrieben haben, aber nehmen wir hier an, dass Sie ein Programm wie das folgende geschrieben haben:
area = f(xl) / 2
for i in range(1, n):
x = ...
area += f(x)
area += f(xu) / 2
...In diesem Programm wird die for-Schleife nicht ausgeführt, wenn
$n = 1$ ist. (Es ist das richtige Verhalten.)
In solchen Sonderfällen
können leicht Fehler gemacht werden.
Im Fall $n = 2$ wird die for-Schleife nur einmal ausgeführt.
Und $n = 16$ ist ein allgemeinerer Fall (bei dem die konkrete Zahl
weniger wichtig ist).
Darüber hinaus wurde auch $n = 1000$ ausprobiert.
Dies wurde gewählt, weil 16 ($= 2^4$) eine besondere
Zahl
für Computer ist1, und deshalb wurde eine weniger
besondere
Zahl gewählt.
Gleichzeitig lässt sich so überprüfen, dass die Berechnung nicht
extrem lange dauert, indem eine etwas größere Zahl verwendet wird.
(Je nach dem Computer, den Sie benutzen, und der Funktion, die Sie
berechnen lassen möchten, wird eine Berechnung mit einer Anzahl der
Teilungen von etwa 1000 höchstwahrscheinlich in einem Augenblick
erledigt.)
$f(x) = x^2$ in Übung 2 ist ein Beispiel, bei dem das Ergebnis von $n$ abhängt.
Nochmals: Wer viele Fehler macht, macht gute Erfahrungen für die Zukunft. Wenn Sie einen Fehler machen, denken Sie langsam darüber nach, was Sie falsch gemacht haben und wie Sie es gemacht haben. Das Sammeln von Erfahrungen mit solchen Fehlern ist ein notwendiger Schritt, um bessere Programme schreiben zu können.
Übungen (2)
Nun versuchen Sie, einige praktische Probleme zu lösen.
Allerdings, wenn Sie das Programm für die obige Übung richtig geschrieben haben, dürfte es kaum nötig sein, etwas anderes als die zu berechnende Funktion zu ändern. (Falls größere Änderungen erforderlich waren, prüfen Sie, warum dies der Fall ist.)
Dafür:
-
In der obigen Formel befindet sich $-\infty$ im Integrationsintervall, so dass sie so nicht numerisch integriert werden kann. Daher betrachten wir zunächst die folgende Formel (Beachten Sie das Integrationsintervall): $$ \int_{-\infty}^0 \frac{1}{\sqrt{2\pi}} \exp\left(-\frac{x^2}{2}\right) \mathrm{d}x $$ Welchen Wert hat diese Formel und warum?
(Hinweis: Sie können diese Frage ohne Berechnung antworten!)
-
Schreiben Sie eine Funktion, um $f(x) = \exp\left(- \frac{x^2}{2}\right)$ zu finden. Zeigen Sie auch den Wert von $f(x)$ bei $x=0, 1/2, 1$ an.
-
Ermitteln Sie mit Hilfe dieser Funktion das Integral mit Hilfe der Trapezformel. Bestimmen Sie das Integral für verschiedene Werte von $a$ und $n$. Vergleichen Sie die erhaltenen Werte mit den wahren Werten.
Die wahren Werten können z. B. auf der folgenden Seite berechnet werden.
-
Keisan Online Calculator > Standard normal distribution Calculator (CASIO COMPUTER CO., LTD.)
-
Im Folgenden sind die Daten eines Spektrums dargestellt, die bei einer Messung gewonnen wurden. Schreiben Sie ein Programm, um die Fläche (Integralwert) dieses Spektrums zu bestimmen. Gehen Sie dabei davon aus, dass die Anzahl der Daten nicht festgelegt ist (und sich ändern kann).
wavelength = [320.0, 320.2, 320.4, 320.6, 320.8, 321.0, 321.2, 321.4,
321.6, 321.8, 322.0, 322.2, 322.4, 322.6, 322.8, 323.0,
323.2, 323.4, 323.6, 323.8, 324.0, 324.2, 324.4, 324.6,
324.8, 325.0, 325.2, 325.4, 325.6, 325.8, 326.0, 326.2,
326.4, 326.6, 326.8, 327.0, 327.2, 327.4, 327.6, 327.8,
328.0, 328.2, 328.4, 328.6, 328.8, 329.0, 329.2, 329.4,
329.6, 329.8, 330.0]
intensity = [6.821, 5.984, 6.159, 6.139, 5.903, 6.048, 6.008, 5.823,
5.376, 5.701, 5.395, 5.225, 5.220, 4.676, 5.028, 4.680,
4.692, 4.355, 4.969, 5.486, 7.238, 8.392, 9.946, 11.86,
13.87, 15.12, 16.22, 16.63, 16.56, 15.96, 13.95, 11.68,
10.04, 7.996, 6.554, 5.097, 4.336, 4.100, 3.695, 3.012,
3.058, 2.864, 2.588, 2.428, 1.931, 1.933, 2.071, 2.053,
1.476, 1.993, 2.058]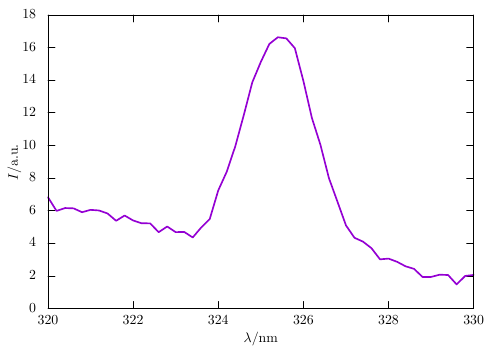
Überprüfen der Ergebnisse (2)
Das Folgende gilt nicht nur für numerische Berechnungen, sondern auch für Berechnungen im Allgemeinen. Vergewissern Sie sich, dass Sie es verstehen.
Bei der letzten Übung ist es im Gegensatz zur ersten etwas schwieriger zu überprüfen, ob das Programm korrekt ist, da der wahre Wert unbekannt ist und daher nicht verglichen werden kann.
In einem solchen Fall sollten Sie
-
mit einfachen Daten berechnen lassen
-
einen ungefähren Wert schätzen und sie vergleichen.
Prüfung mit einfachen Daten
Sie können zum Beispiel mit Datensatz, die leicht zu überprüfen ist (sowohl für die manuelle Berechnung als auch für das Programm), die Ergebnisse überprüfen.
wavelength = [1, 2]
intensity = [1, 1]wavelength = [1, 2, 3]
intensity = [1, 1, 2]
Es ist auch gute Idee, die verwendeten Daten und die
Zwischenergebnisse mithilfe print() anzuzeigen.
Wenn die Daten jedoch zu einfach sind, kann es passieren, dass das Programm mit einem Datensatz zufällig funktionieren, obwohl mit einem anderen jedoch nicht. Daher ist es besser, wenn Sie das Programm mit mehreren verschiedenen Daten ausprobieren.
In den obigen Beispielen handelt es sich im ersten Fall um ein Rechteck und im zweiten Fall um ein zusätzliches Trapez. Es ist auch besser, auf negative Werte, Dreiecke (einschließlich solcher mit einer Intensität von 0) usw. zu achten.
Grobe Schätzung
In der obigen Übung ist es auch möglich, dass Sie das (erwartete) Ergebnis folgendermaßen schätzen.
-
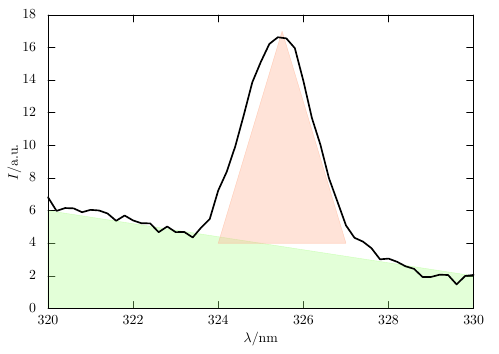
Der untere Teil des Diagramms sieht ungefähr wie ein Trapez aus (der grüne Teil unten), so dass die Fläche dieses Teils etwa $(6 + 2) \times (330 - 320) / 2 = 40$ betragen würde.
-
Der
Berg
ist ein sehr grobes Dreieck (rot). Seine Fläche beträgt dann etwa $(327 - 324) \times (17 - 4) / 2 = 19.5$. -
Die Summe dieser Werte ist 59.5. Wenn der durch das Programm erhaltene Wert nicht allzu weit von 60 entfernt ist, können Sie davon ausgehen, dass Sie ihn vermutlich richtig berechnet haben. Wenn der Wert extrem von 60 abweicht, z. B. 300 oder 10, dann ist das Ergebnis mit hoher Wahrscheinlichkeit falsch.
Dies mag überraschend erscheinen, aber solche einfachen Schätzungen sind in der Praxis oft sehr nützlich.
Sonstige Anmerkungen
Beachten Sie die Grenzen
Wie in Iteration erwähnt,
sollten Sie bei der Verwendung von Schleifen (insbesondere for)
sorgfältig prüfen, ob die Schleifenbedingung korrekt ist.
Einheiten
In der obigen Diskussion wurden Einheiten weggelassen, aber diese Einstellung ist nicht korrekt.
Normalerweise zeigen Programme für numerische Berechnungen nur Zahlen an und kümmern sich nicht um Einheiten. Daher müssen Sie (statt der Programme) die Einheiten (außerhalb des Programms) ergänzen.
Tatsächlich ist die Kombination aus Intervalllänge 1 und der Anzahl der Teilungen $2^4$ eine der Kombinationen ohne $h$-Fehler bei Binärzahlen.