Gepulste Kernspinresonanz an Protonen

Vorbemerkungen

Magnetische Kernspinresonanz (Nuclear Magnetic Resonance) Methoden gehören zu den wichtigsten Analytik-Methoden in der Chemie und sind z.B. bei der Aufklärung molekularer Strukturen unentbehrlich.

Schon mit einem sehr einfachen NMR-Experiment können unterschiedliche Resonanzfrequenzen von Protonen gemessen werden, um daraus etwas über die chemische Zusammensetzung einer Probe zu lernen. Es gibt eine Vielzahl von aufwendigeren NMR-Experimenten, mit denen z.B. die räumliche Anordnung molekularer Strukturen entschlüsselt werden können.

Einen großen Bekanntheitsgrad hat die NMR im medizinischen Bereich als eine der wichtigen bildgebenden Methoden. Mit Hilfe der Kernspintomographie können 3D-Aufnahmen z.B. am menschlichen Körper aufgenommen werden, ohne das ein Eingriff erfolgen muss.

In diesem Praktikumsversuch sollen einige sehr grundlegende Prinzipien aller NMR-Methoden besprochen werden. Mit einfachen NMR Experimenten wird das Verhalten von Protonen in einem statischen Magneten untersucht.

Theoretische Grundlagen

Grundprinzip – Zeeman-Aufspaltung

Viele Atomkerne besitzen einen Eigendrehimpuls \vec{I} (Spin) und damit verknüpft ein magnetisches Moment ^(†) \vec{\mu},

Das gyromagnetische Verhältnis \gamma ist dabei element- und isotopenspezifisch. Wasserstoffatome \ce{^1H} besitzen mit \gamma_{\ce H} = 2\pi\cdot \pu{42,567e6s-1T-1} die größte gyromagnetische Konstante.

Mittels der Kernspinresonanz-Spektroskopie werden die magnetischen Eigenschaften von Atomkernen vermessen. Dazu lässt man die Atomkerne mit externen Magnetfeldern wechselwirken. Im einfachsten Fall wird eine Probe in ein äußeres statisches Magnetfeld \vec B_{0} gebracht. Die Wechselwirkungsenergie zwischen einem Dipolmoment \vec \mu und einem Magnetfeld \vec B_{0} lässt sich klassisch mit E = - \vec{\mu}\cdot\vec B_{0} berechnen. Es ist üblich, die Richtung des äußeren statischen Magnetfelds als z-Achse zu bezeichnen, so dass

Aus einer quantenmechanischen Betrachtung der Wechselwirkung zwischen einem Atomkern und \vec B_{0} folgt, dass nur bestimmte Orientierungen von \vec{\mu} relativ zu \vec B_{0} erlaubt sind. Die Wechselwirkungsenergie kann nur diskrete Werte annehmen,

m ist die magnetische Quantenzahl und kann Werte abhängig von der Kernspinquantenzahl I annehmen,

Für ein Proton \ce{^{1}H} mit einem Kernspin von I = \frac{1}{2} sind damit zwei Energien möglich, E_{\frac{1}{2}} und E_{-\frac{1}{2}}. Die Energiedifferenz der Zustände wird als Zeeman-Aufspaltung bezeichnet

und ist proportional zur Magnetfeldstärke. \ \omega_{L} wird als Larmorfrequenz bezeichnet \left( \omega_{L} = 2\pi \nu_{L} \right).

Eine präzise Beschreibung der Wechselwirkungen von Kernspins mit äußeren Magnetfeldern, aber auch untereinander, ist mit Hilfe der Quantenmechanik möglich.

Wir wollen uns hier auf eine Beschreibung mit einem Vektormodell beschränken, mit dessen Hilfe einfache Zusammenhänge beschrieben werden können. Schon einfache Spin-Spin-Kopplungen (z.B. J-Kopplung) können mit dem Vektormodel nicht mehr beschrieben werden.

Thermisches Gleichgewicht – Boltzmann-Statistik

Wie zuvor beschrieben, können Spins mit I=-1/2 (z.B. \ce{^{1}H}, \ce{^{13}C}) in einem starken Magnetfeld zwei verschiedene Zustände einnehmen, die zwei verschiedenen, entgegengesetzten Projektionen auf die z-Achse entsprechen. Von einem einzelnen Spin sind nur die z-Komponente \mu_{z} und die Länge \left| \vec{\mu} \right| = \sqrt{\mu_{x}^{2} + \mu_{y}^{2} + \mu_{z}^{2}} bestimmt.

Für ein Ensemble von Spins bedeutet dies, dass im thermischen Gleichgewicht ein Teil der Spins (m = \ + \frac{1}{2}) zu einer Magnetisierung in z-Richtung beitragen, der Rest (m = \ - \frac{1}{2}) genau entgegen gesetzt. Aufgrund der Boltzmannbesetzung der beiden Zustände

resultiert eine effektive Gesamtmagnetisierung \vec{M} = \sum_{i}^{}{\vec{\mu}}_{i} > 0 der Probe in z-Richtung. Für unseren Praktikumsmagneten mit \omega_{L} \approx 2\pi \cdot \pu{20MHz} folgt aus Gleichung (6) bei Raumtemperatur \frac{N_{-}}{N_{+}} = 0.99999672. Die Besetzungsunterschiede und damit die Gesamtmagnetisierung |\vec{M}| sind demzufolge sehr gering.

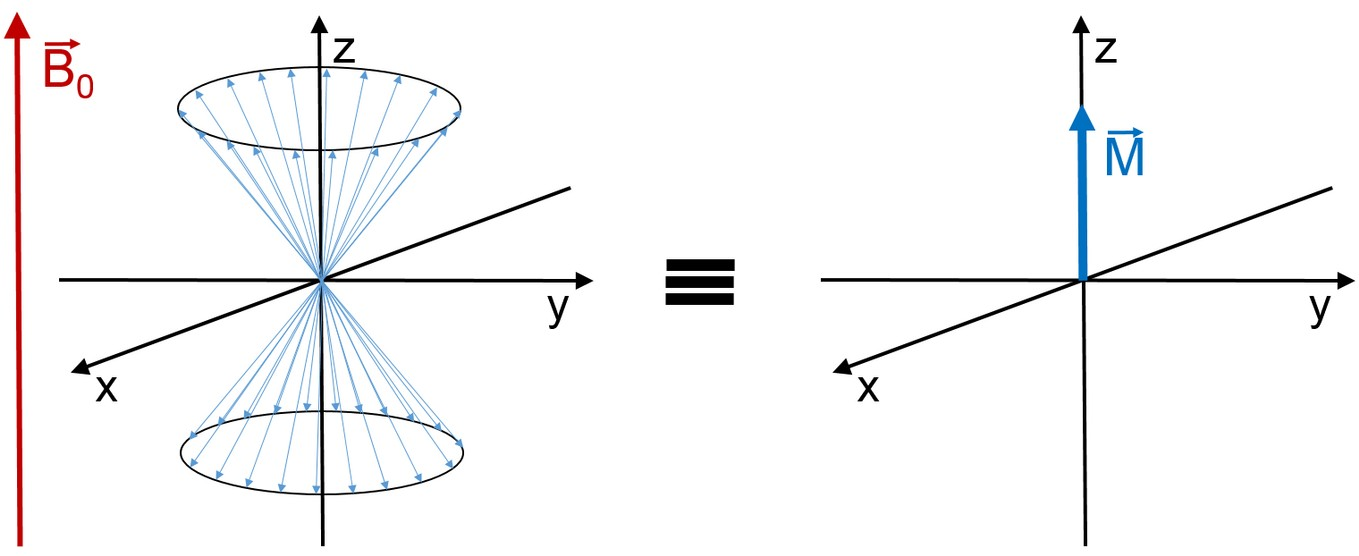
Für einfache NMR-Experimente lässt sich die Summe aller Spins mit einem Vektormodell beschreiben, daher soll dies im Folgenden weiterverwendet werden.

Ein einfaches NMR Experiment

Um ein NMR-Experiment durchzuführen, muss ein weiteres Magnetfeld senkrecht zu \vec B_{0} auf die Probe eingestrahlt werden. Dazu ist eine Hochfrequenzspule eingebaut, die ein oszillierendes Magnetfeld \vec B_{1} (t) erzeugen kann.

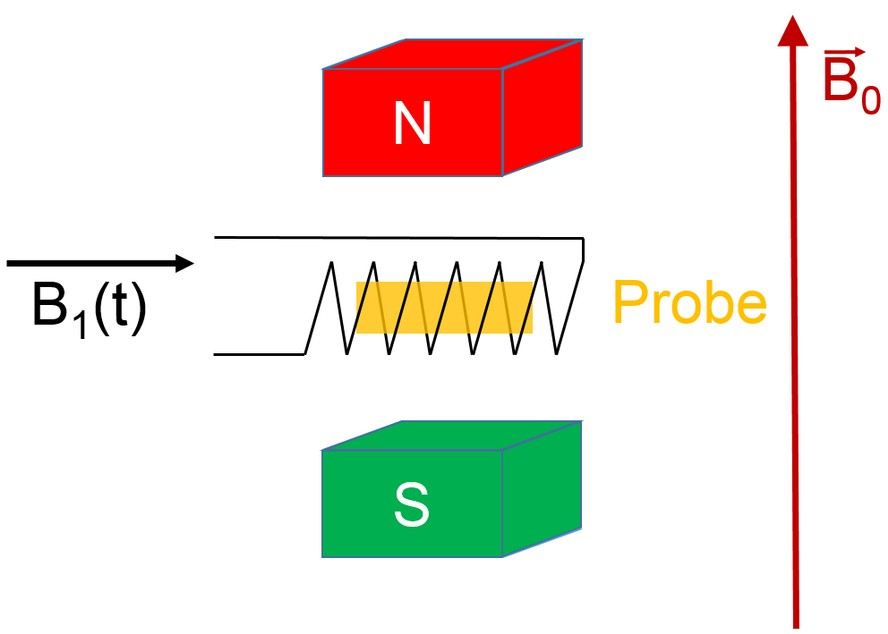
Wird an eine Probe ein Hochfrequenzpuls mit der passenden Frequenz \omega_{\text L} angelegt, können Übergänge zwischen den Energieniveaus der Kernspins induziert (stimuliert) werden.

Die Wirkung von einem sogenannten 90\degree-Puls entspricht einer Drehung der Gesamtmagnetisierung um 90\degree und kann mit dem Vektormodell, allerdings nach einem weiteren Schritt, sehr einfach dargestellt werden.

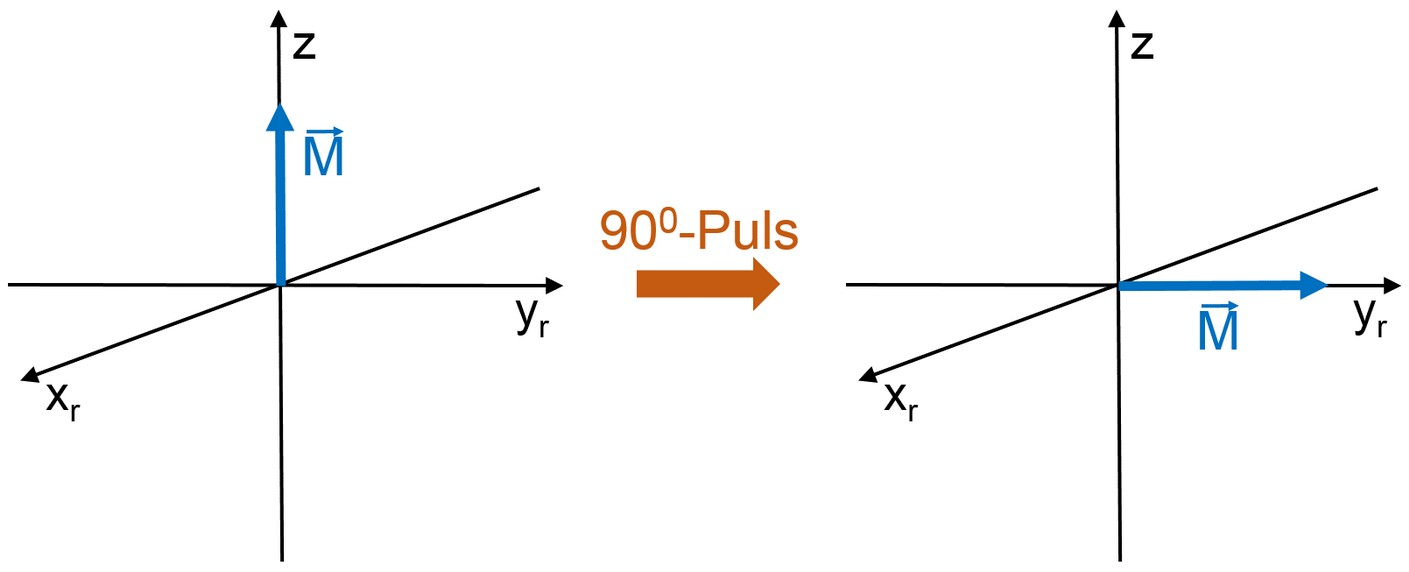
Tatsächlich präzedieren die Spins nach dem HF-Puls kohärent mit der Larmorfrequenz um die z-Achse. Auch die Magnetisierung \vec{M} nach einem HF-Puls präzediert entsprechend. Wenn wir als Beobachter uns nun auch mit der gleichen Frequenz um die z-Achse drehen, erscheint die Magnetisierung \vec{M} wieder zeitunabhängig. Es wird eine Transformation vom Laborkoordinatensystem (x,y,z) in ein rotierendes Koordinatensystem (x_{r},y_{r},z) durchgeführt. Eine sehr einfache Analogie ist das Betrachten eines sich drehendes Karussells. Im Laborkoordinatensystem kommen die Kinder immer wieder an einem vorbei. Wenn man nun aber neben dem Karussell in der passenden Geschwindigkeit mitläuft, bewegen sich die Kinder nicht mehr relativ zum Betrachter.

Die nach einem 90\degree-Puls präzedierende makroskopische Magnetisierung induziert in der HF-Spule eine mit \omega_{\text L} oszillierende Spannung U(t) \propto \cos(\omega_{\text L}t), die kernmagnetische Induktion, die gemessen werden kann.

Mathematisch kann die Transformation in ein rotierendes Koordinatensystem durch eine einfache Multiplikation der gemessenen Spannung U(t) mit \cos(\omega_{\text r}t) durchgeführt werden.

Nur die niederfrequente Komponente mit \omega = \omega_{\text L} - \omega_{\text r} wird weiter verarbeitet, die hochfrequente Komponente mit \omega = \omega_{\text L} + \omega_{\text r} wird üblicherweise mit einem Tiefpass herausgefiltert. Wenn sich das rotierende Koordinatensystem mit der Präzessionsfrequenz dreht, d.h. \omega_{\text L}= \omega_{\text r}, folgt U_{r}(t) \approx \frac{U_{0}}{2}, ein zeitlich konstantes Signal.

Wenn nun das rotierende Koordinatensystem nicht exakt der Präzessionsfrequenz entspricht, d.h. \omega_{\text L}\neq \omega_{\text r}, wird ein Signal erhalten, welches mit der Differenzfrequenz oszilliert, U_{r}(t) \approx \frac{U_{0}}{2}\cos\left( \left( \omega_{\text L}- \omega_{\text r} \right) t \right). In der einfachen Analogie würde dies bedeuten, dass man etwas langsamer (oder etwas schneller) neben dem Karussell läuft. Die Kinder bewegen sich relativ zum Betrachter, aber nur mit der Differenzgeschwindigkeit.

Verschiedene Effekte führen dazu, dass die kernmagnetische Induktion mit der Zeit kleiner wird. Dieser Zerfall der Magnetisierung in der x,y-Ebene wird als free induction decay FID bezeichnet und entweder durch Relaxationsprozesse in der Probe oder durch unterschiedliche „lokale“ Übergangsfrequenzen \omega_{\text L} verursacht.

Der einfachste Grund für unterschiedliche „lokale“ Übergangsfrequenzen \omega_{L} liegt in der Magnetfeldinhomogenität, die praktisch jeder Magnet hat. Normalerweise wird in NMR-Magneten versucht, diese Inhomogenität zu minimieren, wozu mit zusätzlichen Spulen magnetische Ausgleichsfelder erzeugt werden. Dieser Vorgang wird shimmen genannt.

Magnetfeldinhomogenitäten bedeuten, dass an verschiedenen Orten in der Probe unterschiedliche Magnetfelder vorliegen und dadurch auch die Larmorfrequenzen \omega_{L} unterschiedlich sind. Da aber das rotierende Koordinatensystem sich genau nur mit einer Frequenz \omega_{r} drehen kann, beobachtet man in einem NMR-Experiment nach einem 90\degree-Puls eine Dephasierung der Gesamtmagnetisierung.

Einfluss der Pulslänge auf FID-Intensität

Im thermodynamischen Gleichgewicht besitzt eine NMR-Probe eine Gesamtmagnetisierung nur in z-Richtung. Um mit einem einzelnen HF-Puls eine maximale FID-Intensität zu erhalten, muss der HF-Puls bei einer bestimmten Leistung eine bestimmte Dauer haben. Typischerweise ist die Leistung vorgegeben, so dass nur die Zeitdauer des HF-Pulses variiert werden kann. Diese wird nun so eingestellt, dass maximale FID-Intensität gemessen wird. Dann entspricht die Wirkung des Pulses einer 90° Drehung, wie es in Abbildung 3 dargestellt wird. Würde nun der einzelne HF-Puls doppelt so lange dauern, entspräche die Wirkung effektiv einer Drehung der Magnetisierung um 180°, es wäre nur Magnetisierung in z-Richtung vorhanden und damit kein Signal in der Spule (Abbildung 2) messbar.

Nehmen wir mal an, dass beispielsweise die optimale Pulslänge 10\mu s beträgt, um die Magnetisierung um 90° zu drehen. Dann würde eine Pulslänge von 20\mu s kein FID erzeugen. Eine Pulslänge von 30\mu s würde hingegen die Magnetisierung um 270° drehen, so dass nun ein maximaler negativer FID resultieren würde. Bei einer Pulslänge von 40\mu s hätten wir um 360⁰ gedreht und die Gesamtmagnetisierung würde wieder in +z-Richtung zeigen (→ kein FID). Pulslängen dazwischen würden zu kleineren FID-Intensitäten führen.

Spektrum eines Hochfrequenzpulses

Um gleichzeitig verschiedene Frequenzen auf eine Probe zu strahlen, reicht es normalerweise aus, einen Puls mit nur einer Frequenz auszusenden. Tatsächlich beinhaltet dieser Puls dann ein ganzes Spektrum an Frequenzen (siehe Anhang).

Um die Frequenzkomponenten dieses Zeitsignals zu erhalten, muss eine Fourier-Transformation durchgeführt werden. Damit kann ein Signal in einen reziproken Bereich umgewandelt werden. Hier wird ein Zeitsignal [s] in ein Frequenzsignal [s^{- 1}] transformiert. Diese Transformation ist verlustfrei, d.h. das Frequenzsignal beinhaltet die vollständige Information wie das Zeitsignal, es kann beliebig oft zwischen beiden hin und her transformiert werden, ohne dass sich das Signal verändert.

Wenn der Puls aus Abbildung unendlich lang wird, ergibt die Fourier-Transformation eine scharfe Linie (Delta-Funktion) bei \pu{20 MHz}. Je kürzer der Hochfrequenzpuls ist, desto breiter wird die Linie (Spektrum).

Ein Puls mit einer Länge von \Delta t = \pu{1 \mu s} erzeugt ein Spektrum mit einer \text{FWHM} = \pu{1.2 MHz}, ein zehnmal längerer Puls \Delta t = \pu{10\mu s} korrespondiert zu einem Spektrum mit \text{FWHM} = \pu{120 kHz}. Die Form des Spektrum mit den Nebenmaxima wird durch die Fourier-Transformation einer Rechteckfunktion bestimmt (\left| \frac{\sin(x)}{x} \right|).

Für das NMR-Experiment bedeutet dies, dass mit einem \pu{10\mu s} langen Hochfrequenzpuls (\pu{20 MHz}) Kerne im Bereich von \pu{19.940 MHz - 20.060 MHz} effektiv angeregt werden können.

Chemische Verschiebung – NMR Spektrum

Wenn das externe Magnetfeld B_{0} bekannt ist, kann die Resonanzfrequenz jedes Protons nach Gleichung 5 berechnet werden. Dies gilt aber nur, wenn die nackten Kerne vorliegen. In Atomen erzeugen die Elektronen magnetische Zusatzfelder, die am Atomkern eine Verstärkung oder eine Abschwächung (Abschirmung) des externen Magnetfeldes bewirken.

Bei der Abschirmung induziert das äußere (externe) Magnetfeld B_{0} mit den Elektronen ein sekundäres Feld B_{\text{ind}}, welches dem äußeren Feld entgegengesetzt ist. Am Kernort liegt daher ein effektives Feld B_{\text{eff}} an,

Die Abschirmkonstante \sigma hängt nun von der Elektronendichte um einen Kern ab. Je höher sie ist, umso größer ist \sigma. Ein kleineres magnetisches Feld bedeutet eine kleinere Zee_­man-Aufspaltung (Gleichung 5), so dass aus der Abschirmung eine Frequenzverschiebung zu niedrigeren Frequenzen um

folgt. Um eine Abschirmkonstante aus einer gemessenen Frequenz zu ermitteln, müsste in einem NMR-Spektrometer \omega_{0} sehr genau bekannt sein. Tatsächlich werden in der NMR keine absoluten \sigma ermittelt, sondern Abschirmkonstanten relativ zu einer Referenzsubstanz mit einem \sigma_{\text{ref}}. Die Resonanzfrequenz der Referenzsubstanz ist

Die Resonanzfrequenz einer Probe \omega_{\text{probe}}\ relativ zur \omega_{\text{ref}} Referenz wird in Form der chemischen Verschiebung \mathbf{\delta} bestimmt (\sigma \ll 1),

Als Referenzsubstanz wird sehr häufig Tetramethylsilan TMS verwendet. Es hat 12 equivalente Protonen, d.h. alle Protonen haben die gleiche Elektronendichte am Kernort und damit die gleiche Abschirmkonstante. Ein weiterer Grund für die Wahl von TMS als Referenzsubstanz ist, dass die Abschirmung der Protonen in TMS größer ist als in den meisten anderen organischen Verbindungen, \sigma_{\text{TMS}} > \sigma_{\text{probe}}. Da die chemische Verschiebung generell sehr klein ist, wird sie in \text{ppm} (parts per million) angegeben.

Für Protonen \ce{^{1}H} liegt \delta im Bereich von \pu{0 ppm} bis \pu{15 ppm}.

Um die chemischen Verschiebungen in einer Probe zu messen, genügt es, mit einem einfachen 90\degree-Puls die Probe anzuregen. Danach befindet sich die Gesamtmagnetisierung in der xy-Ebene (Abbildung 3) und beginnt nun zu dephasieren (Abbildung 4). In der Spule wird dadurch eine Spannung induziert (FID), die danach weiterverarbeitet wird.

Da die aufgezeichnete Spannung noch mit der Hochfrequenz oszilliert, erfolgt zuerst die Transformation in das rotierende Koordinatensystem.

Beispiel:

Es wird eine Mischung aus 99\% Benzol und 1\% TMS gemessen. TMS dient als Referenzsubstanz.

Jetzt nehmen wir an, dass aufgrund der Magnetfeldstärke die Protonen von TMS eine Resonanzfrequenz von \omega_{\text{ref}} = 2\pi\cdot\pu{20,000000 MHz} haben. Dann haben die Protonen von Benzol in dem gleichen Magneten eine Resonanzfrequenz von \omega_{\text{benzene}} = 2\pi\cdot\pu{20,000146MHz}. Eingesetzt in Gleichung 11 ergibt dies eine chemische Verschiebung von \delta = \pu{7.3 ppm}.

Für die Anregung der Probe wird ein \pu{10 \mu s} langer Puls mit \pu{20,000 MHz} in die Mischung eingestrahlt, mit dem Kerne im Bereich von \pu{19,940 MHz - 20,060 MHz} angeregt werden können (siehe Abschnitt 2.4).

Der Frequenzbereich ist breit genug, um alle Protonen in Benzol und TMS anzuregen. Danach emittieren beide, mit \pu{20,000000 MHz} und mit \pu{20,000146 MHz}. Jetzt wird in das rotierende Koordinatensystem transformiert, welches mit \pu{20,000000 MHz} dreht. Effektiv wird von den aufgezeichneten Frequenzen \pu{20,000000 MHz} abgezogen, so dass TMS in dem rotierenden Koordinatensystem nun eine Frequenz von \pu{0 Hz} und Benzol eine Frequenz von \pu{146 Hz} aufweisen.

Um die auftretenden Frequenzen in dem Zeitsignal zu identifizieren, wird eine Fourier-Transformation durchgeführt (siehe Anhang). Damit wird ein Zeitsignal [\mathrm s] in ein Frequenzsignal [\mathrm s^{- 1}] transformiert.

Relaxation in das thermische Gleichgewicht

Im thermodynamischen Gleichgewicht sind die beiden Zeeman-Energieniveaus eines Protons entsprechend der Boltzmann-Statistik besetzt (Gleichung 6). Durch das Einstrahlen von Hochfrequenzpulsen in einem NMR-Experiment wird die Gleichgewichtsbesetzung gestört, das Spin-System muss danach wieder in das thermodynamische Gleichgewicht relaxieren, d.h. das ursprüngliche Boltzmann-Gleichgewicht stellt sich wieder ein. Je effektiver das Spin-System an die Umgebung gekoppelt ist, desto schneller wird die Relaxation stattfinden. Aufgrund dieser Kopplung Spin↔︎Umgebung wird diese Relaxation oft Spin-Gitter-Relaxation genannt. Die dazugehörende Zeitkonstante wird mit T_{1} bezeichnet. Manchmal wird auch der Begriff longitudinale Relaxation verwendet. Als longitudinal wir die z-Achse bezeichnet (siehe Abbildung 3), transversal wäre in der \text{xy}-Ebene.

Es gibt verschiedene Möglichkeiten, die Zeitkonstante T_{1} zu messen. Wenn die Probe sich im Gleichgewicht befindet, kann mit einem 180\degree-Puls die Gesamtmagnetisierung um 180\degree gedreht (invertiert) werden.

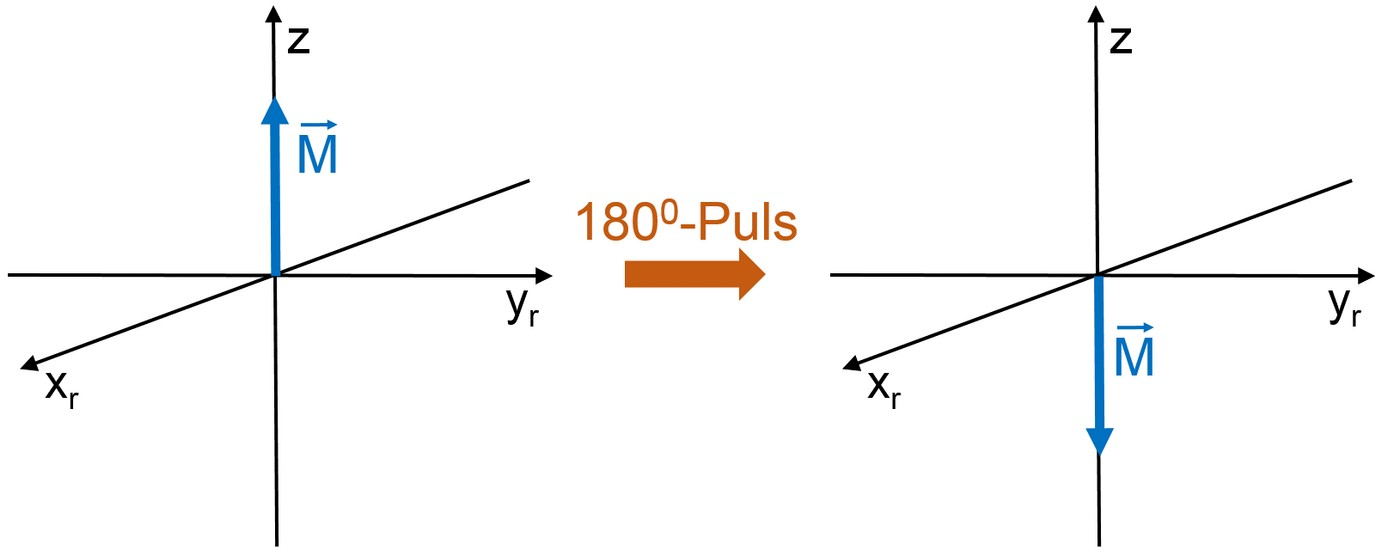
Dass bedeutet, es befinden sich mehr Spins in dem energetisch höheren anstatt im niedrigeren Zustand. Daher muss das Spin-System zum Relaxieren Energie an die Umgebung (Gitter) abgeben. Die Magnetisierung \vec{M} relaxiert wieder in das Boltzmann-Gleichgewicht.

Diesen Zeitverlauf der Relaxation kann man nicht in einem einzelnen Experiment messen. Stattdessen wird der Zeitverlauf dadurch erhalten, dass nach Störung der Gleichgewichtsmagnetisierung (z.B. mit 180\degree-Puls) die sich ändernde Magnetisierung nach einer Zeit t_{i} abgefragt wird. Dies wird für verschiedene Zeiten t_{i} wiederholt.

Die Abfrage der Magnetisierung erfolgt mit einem zweiten Puls, einem 90\degree-Puls, der die longitudinale Magnetisierung in die xy-Ebene dreht und erst dann ein Signal in der Spule erzeugt. Die Amplitude der Magnetisierung folgt einem exponentiellen Zeitgesetz und wird hier mit

beschrieben. M_{0} ist die Gleichgewichtsmagnetisierung, M(t \rightarrow \infty) = M_{0}.

Die Geschwindigkeitskonstante T_{1} hängt unter anderem von der Bewegung der Moleküle in der Probe ab! Übergänge zwischen Kernspinzuständen erfolgen, in dem die passende Energie (Frequenz) eingestrahlt wird. Genau dies erfolgt, wenn über die HF-Spule ein Hochfrequenzpuls eingestrahlt wird. Tatsächlich erfolgen aber auch ohne eingestrahltem HF-Feld Übergänge, aber durch die Protonen untereinander. Bewegt sich ein Molekül in der Nachslashschaft von einem Proton, fluktuieren an dem Ort des Protons Magnetfelder. Diese Fluktuationen sind typischerweise stochastisch und beinhalten verschiedene Frequenzen (ein Frequenzspektrum), darunter auch mehr oder weniger Anteile bei \pu{20 MHz}. Eine besonders effektive Spin-Gitter-Relaxation, d.h. ein besonders kurzes T_{1}, erhält man, wenn die Bewegungen der Moleküle (Rotation, Translation) besonders viel „\pu{20 MHz}“ beinhalten. Ein schönes Beispiel ist Glyzerol, welches schon bei Raumtemperatur sehr viskos ist und bei dem relativ viele Anteile an „\pu{20 MHz}“ vorliegen. Es gibt genau eine Temperatur, bei der die Molekülbewegung in Glyzerol optimal passt, dann hat T_{1} seinen kleinsten Wert. Bei anderen Temperaturen bewegen sich die Moleküle entweder langsamer oder schneller, der Anteil an der „\pu{20 MHz}“-Komponente sinkt und T_{1} wird wieder länger.

Das Spin-Echo

Die nach einem 90\degree-Puls erfolgende Dephasierung der Magnetisierung in der xy-Ebene (Abbildung 4) ist zum Teil reversibel! Insbesondere Dephasierung aufgrund von Magnetfeldinhomogenitäten kann wieder rückgängig gemacht werden. Dazu muss nach dem 90\degree-Puls ein weiterer 180\degree-Puls eingestrahlt werden.

Nach dem ersten Puls dephasiert die Magnetisierung, bis zum Zeitpunkt t_{a} ein Echo-Puls eingestrahlt wird. Da das Rephasieren genauso lange dauert wie das Dephasieren, erfolgt zum Zeitpunkt 2t_{a} das Echo-Signal.

Versuchsaufbau

Hardware

Das im Praktikum verwendete NMR-System ist ein vollwertiges Kernspinresonanz-Spektrometer, mit dem sogar 3D-Tomographieaufnahmen möglich sind. Als Magnet wird ein Permanentmagnet verwendet. Neben einer geringen Magnetfeldstärke ist die Temperaturabhängigkeit der Feldstärke ein Nachteil.

Das Spektrometer ist über ein USB-Kabel mit einem Computer verbunden und wird mittels einer speziellen Software gesteuert.

Software

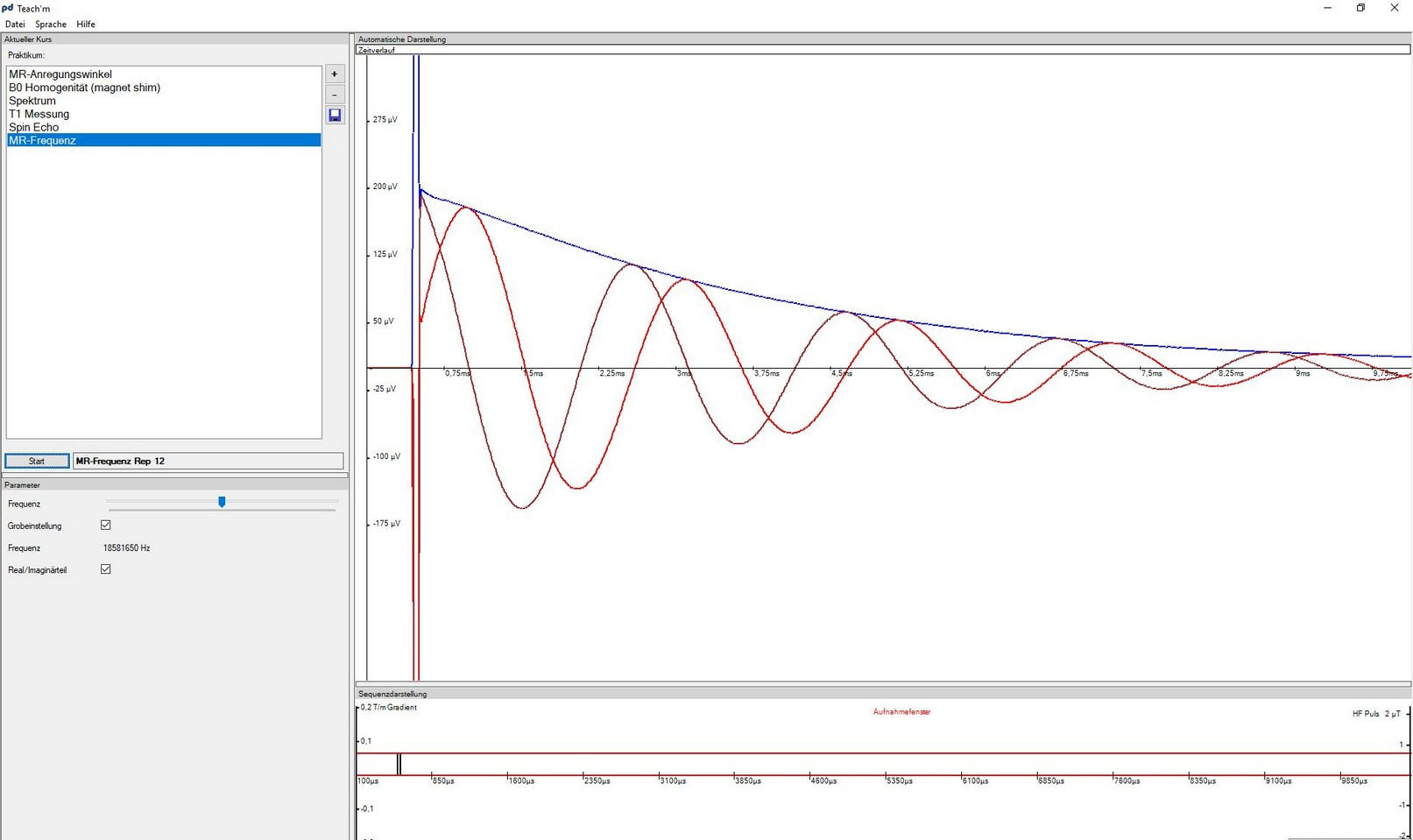
Die verwendete Software pd Teach’m steuert vollständig das NMR-Spektrometer und wertet die aufgezeichneten Daten aus.

Praktikumsaufgaben: Durchführung und Auswertung

Zur virtuellen Durchführung

Es werden verschiedene NMR-Experimente durchgeführt, für die teilweise unterschiedliche Proben und auch NMR Messprotokolle verwendet werden.

Resonanzfrequenz von Glycerol

Bestimmen Sie die Resonanzfrequenz von Glycerol und berechnen Sie daraus u.a. das entsprechende Magnetfeld B_{\text{eff}}. Führen Sie diesen Versuch am Anfang und am Ende des Praktikumstages durch.

Messprotokoll	MR-Frequenz
Probe	Glycerol
Durchführung	Variieren Sie die Frequenz mit dem Schieberegler entweder mit der Maus oder noch besser, mit den Pfeiltasten. Das Zeitsignal oszilliert mit der Differenzfrequenz zwischen eingestellter MR-Frequenz und der Resonanzfrequenz der betrachteten Kerne. Die Resonanzfrequenz ist gefunden bei minimaler Abweichung zwischen blauer und brauner Kurve.
Auswertung	Notieren Sie die Frequenz und berechnen Sie daraus die B_{\text{eff}} und die Zeeman-Aufspaltung als \omega_{\text{eff}} und E_{\text{eff}}. Schätzen Sie ab, wie genau die Resonanzfrequenz bestimmt werden kann und diskutieren Sie die Änderung der Frequenz im Laufe des Versuchtages.
Ergebnisse	Uhrzeit 1: \nu_\text{eff} = \omega_\text{eff} = B_\text{eff} = E_\text{eff} = Uhrzeit 2: \nu_\text{eff} = \omega_\text{eff} = B_\text{eff} = E_\text{eff} =

90°-Pulslänge

Die Probe wird mit einem Puls angeregt und die Signalstärke abhängig von der Pulslänge bestimmt.

Messprotokoll	MR-Anregungswinkel
Probe	Glycerol
Durchführung	Variieren Sie die Pulslänge mit dem Schieberegler und bestimmen Sie per Auge oder mit einem Lineal die Signalintensität (blaue Kurve). Notieren Sie die Pulslängen bei (a) maximalem positiven Signal. Danach verlängern Sie sukzessive die Pulslänge bis das Signal minimal wird (b). Suchen Sie auch die Pulslänge für ein maximal negatives Signal (c).
Auswertung	Notieren Sie alle drei Pulslängen, erklären Sie die und stellen Sie danach wieder die Pulslänge für den 90\degree-Puls ein!
Ergebnisse	t_1 = t_2 = t_3 =

Shimmen

Optimieren Sie die Homogenität des Magneten mit Hilfe der drei Shim-Spulen in X,Y,Z-Richtung. Die Shim-Spulen erzeugen elektromagnetisch zusätzliche Magnetfeldgradienten, mit denen Inhomogenitäten des Permanentmagneten ausgeglichen werden sollen.

Messprotokoll	B0 Homogenität (magnet shim)
Probe	Glycerol
Durchführung	Variieren Sie die Gradienten in x, y, und z–Richtung derart, dass der FID (blaue Kurve) möglichst langsam zerfällt.
Auswertung	Notieren Sie die Einstellungen der Shim-Spulen. In welchen Einheiten wird die Inhomogenität angegeben?
Ergebnisse	\frac{\mathrm dB_0}{\mathrm dx} = \frac{\mathrm dB_0}{\mathrm dy} = \frac{\mathrm dB_0}{\mathrm dz} =

Chemische Verschiebung

Bestimmen Sie die chemische Verschiebungen von Benzol und Cyclohexan und berechnen Sie mit B_{\text{ref}} bzw. \omega_{\text{ref}} (aus 3.1) die dazu gehörenden Resonanzfrequenzen.

Messprotokoll	Spektrum
Proben	Benzol/TMS, Cyclohexan/TMS
Durchführung	Nehmen Sie pro Probe mindestens 20 Spektren auf und mitteln Sie darüber.
Auswertung	Bestimmen Sie die chemischen Verschiebungen. Durch Anklicken der Peakmaxima werden die Werte angezeigt. Diskutieren Sie den Unterschied zwischen Benzol und Cyclohexan. Warum zeigt Cyclohexan nur ein Maximum?
Ergebnisse	\delta_\text{Benzol}= \delta_\text{Cyclohexan}=

T₁-Relaxation

Bestimmen Sie, wie lange es dauert, bis sich die Besetzung der beiden Energieniveaus (der Protonen) nach Boltzmann im thermodynamischen Gleichgewicht befindet.

Messprotokoll	T1-Messung
Proben	Glycerol, Ethylenglykol
Durchführung	Variieren Sie die Einstellparameter so, dass die Relaxationskurve deutlich zu erkennen ist. Die Wartezeit zwischen den Experimenten (Repetitionszeit) sollte mindestens 5 T_{1} betragen. Weiterhin sollten mindestens 20 Punkte aufgezeichnet werden.
Auswertung	Nach der Messung öffnet sich mit einem rechten Mausklick im Datenfenster ein Auswahlmenü. Jetzt sollte → Auswertung → Absolut ausgewählt werden. Es öffnet sich ein neues Fenster, in dem oben links „T1: a-b*e^x/T1“ ausgewählt werden muss. Durch Anklicken von „Kurve anpassen“ erhält man nun den T1-Wert der Messung Warum unterscheiden sich die Relaxationszeiten von Glycerol und Ethylenglykol? Glycerolmoleküle „drehen“ sich bei Raumtemperatur mit \sim \pu{50MHz}. Bewegen sich Ethylenglykolmoleküle schneller oder langsamer bei Raumtemperatur? Wie wirkt sich das auf T_1 aus?
Ergebnisse	Cyclohexan t_\text{repetition}= \Delta t_\text{Punkte}= N_\text{Punkte}= T_{1}= Ethylenglykol t_\text{repetition}= \Delta t_\text{Punkte}= N_\text{Punkte}= T_{1}=

Hahn-Echo

Mit einem Hahn-Echo kann ein Teil des dephasierten Signals wieder rephasiert werden. Erzeugen Sie nun ein Hahnecho und bestimmen Sie den Pulsabstand, bei dem die Echo-Amplitude den halben Wert der Amplitude bei t \rightarrow \pu{0ms} beträgt.

Messprotokoll	Spin Echo
Proben	Glycerol
Durchführung	Stellen Sie die Dauer des 180\degree-Pulses auf den doppelten Wert des 90\degree-Pulses und starten Sie die Messung.
Auswertung	Bestimmen Sie die Echohöhe bei einer Echozeit von \pu{1ms}. Variieren Sie die Echozeit und bestimmen Sie die Echohöhe durch Anklicken. Notieren Sie die Echozeit, bei der die Echohöhe den halben Wert der maximalen Echo annimmt.
Ergebnisse	t_\text{50\%}=

Mit zunehmendem Echoabstand wird das Echosignal kleiner, da nur reversible Anteile der Dephasierung zum Echo beitragen.

Verschlechtern Sie nun mit Hilfe des NMR Messprotokolls aus 3.3 die Magnetfeldhomogenität und führen Sie danach noch einmal das Spin Echo-Experiment durch.

Vorbereitung

Für das Vorgespräch mit dem Betreuer vor dem Praktikumsversuch sollten Sie das vorliegende Skript verstanden haben und Fragen bezüglich der Theorie und Aufbau des NMR-Spektrometers sowie zur Funktionsweise des Geräts beantworten können.

Nach Beendigung des Versuchs ist ein Versuchsprotokoll anzufertigen und dem Betreuer digital (per email) und schriftlich zu übergeben.

Das Versuchsprotokoll sollte sich aus einem kompakten Theorieteil, der Durchführung und der entsprechende Auswertung mit Fehlerdiskussion zusammensetzen.

Literatur

• H. Friebolin, Ein- und zweidimensionale NMR-Spektroskopie: Eine Einführung, Wiley-VCH, 5. Auflage 2013

• S. Bienz, L. Bigler, T. Fox, H. Meier, Spektroskopische Methoden in der organischen Chemie, Thieme, 9. Auflage 2016

• P. W. Atkins, Physikalische Chemie, Wiley-VCH, 5. Auflage 2013

Anhang: Zeit und Frequenz

Ein Hochfrequenzpuls beinhaltet nicht nur die eine Frequenz der Hochfrequenz, sondern auch noch weitere Anteile, die durch die Einhüllende bestimmt werden.

Hier soll nun (sehr kurz) eine Idee vermittelt werden, wie Zeitsignal und Frequenzsignal voneinander abhängen können.

Es wird mit einem sehr einfachen Zeitsignal mit genau einer Frequenz \omega_{1}begonnen. Das Signal in der Zeitdomäne ist eine einfache \sin(\omega_{1}t) (oder \cos(\omega_{1}t)) Funktion. Da nur eine Frequenz \omega_{1} vorliegt, entspricht dies in der Frequenzdomäne einer delta-Funktion bei \omega_{1}:

Im Frequenzspektrum ist genau eine scharfe Linie zu sehen.

Nun besteht das Zeitsignal aus einer Überlagerung von zwei Frequenzen mit \omega_{2} = 3\ \omega_{1} und den Amplituden A_{2} = \frac{A_{1}}{3}:

Das dazu korrespondierende Spektrum besteht aus zwei scharfen Linien. (Hinweis: Schieberegler in der Abbildung auf 2 stellen.)

Bei einer Überlagerung von zehn Frequenzen \left\lbrack \omega_{k} = (2k - 1)\omega_{1};k = 1,2,\ldots,10 \right\rbrack mit passenden Amplituden \left\lbrack A_{k} = \frac{A_{1}}{(2k - 1)} \right\rbrack ist eine Rechteckform schon sehr deutlich zu erkennen. (Hinweis: Schieberegler in der Abbildung auf 10 stellen.)

Das Rechtecksignal hat eine (Wiederhol-) Frequenz von \omega_{1}. Jede \frac{1}{\omega_{1}} Sekunde kommt ein Rechteck. Tatsächlich stecken in dem Rechtecksignal aber viel mehr Frequenzen!

Gefährdungsbeurteilung des Versuches

Chemikalien

Während des Versuches werden verschiedene chemische Substanzen vermessen, die ein unterschiedliches Gefährdungspotential aufweisen. Sämtliche Proben befinden sich entweder in abgeschmolzenen Ampullen oder aber in verschlossenen Reagenzgläsern.

• Glycerol
• Ethylenglycol
  
  H: 302‐373
  P: 301+312+330
• Tetramethylsilan
  
  H: 224
  P: 210
• Benzol
  
  H: 225‐304‐315‐319‐340‐350‐372‐412
  P: 201‐210‐280‐308+313‐370+378‐403+235
• Cyclohexan
  
  H: 225‐304‐315‐336‐410
  P: 210‐240‐273‐301+330+331‐302+352‐403+233

Eine Gefährdung besteht nur, wenn ein Probengefäß zerstört wird.

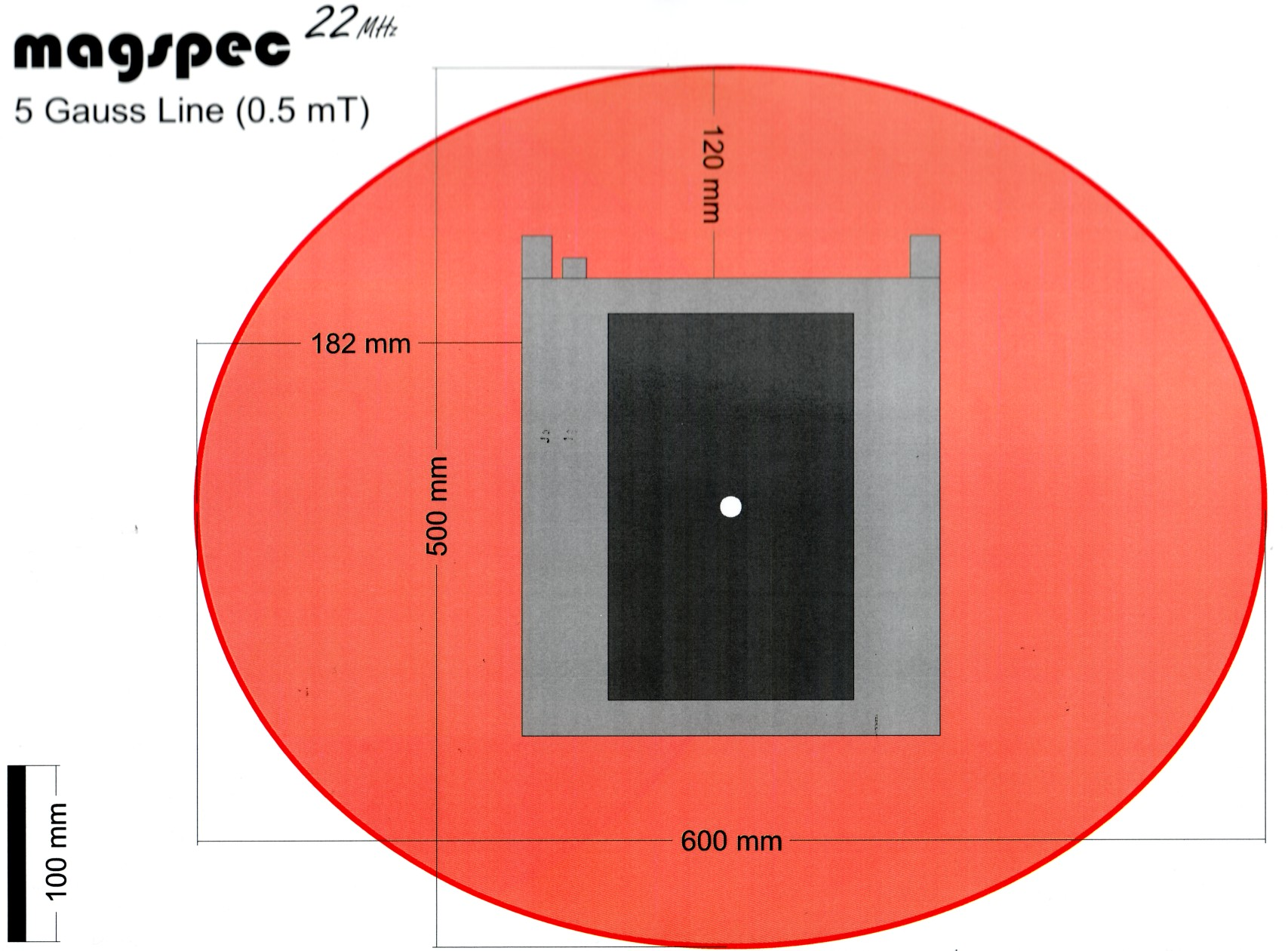
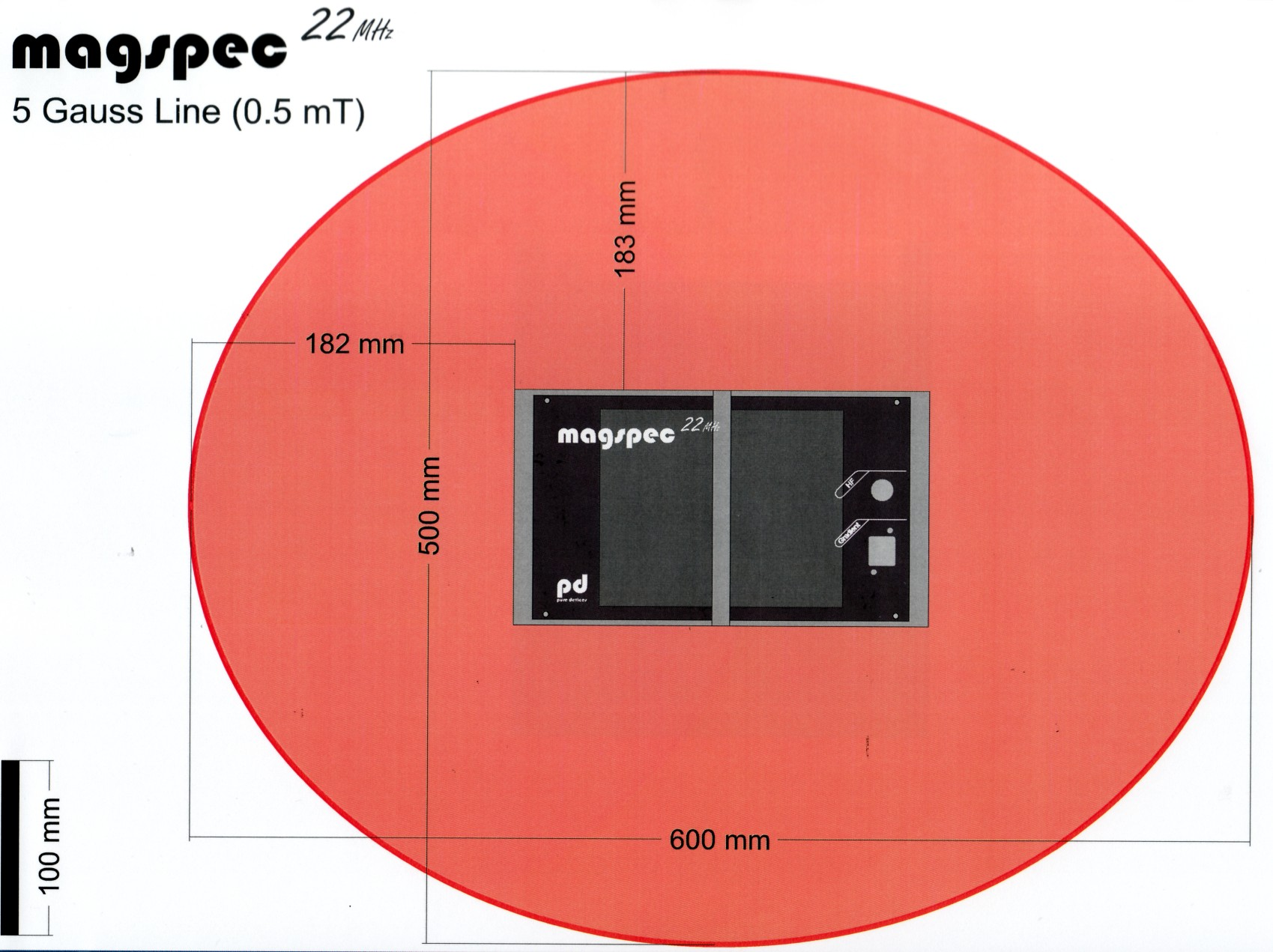
Magnetfeld

Der verwendete Permanentmagnet des NMR – Spektrometers stellt eine mögliche Gefährdung für Personen mit Herzschrittmachern oder Defibrillatoren oder schwangere Frauen dar. Diese dürfen unter keinen Umständen näher als die 5 Gauss–Linie an den Magneten.