Atomic force microscopy - Advanced lab course physical chemistry

Summary

The atomic force microscope (AFM) is an important instrument in surface sience, since the surface of all solid samples (including non-conducting samples) can be imaged in real space. Modern AFM devices allow to resolve individual atoms on the surface of solids and at the solid-liquid interface.

The basic working principle of the AFM is to measure the force acting between a tip and the sample. From this force, information on the properties of the sample can be obtained. If the measurement tip is scanned across the surface, the surface can be imaged based on local differences in the force between tip and sample.

The AFM was invented in 1986 by Gerd Binnig, Calvin Quate and Christoph Gerber. The authors were able to detect the force between tip and sample by attaching the tip to the free end of a cantilever and measuring the deflection of the cantilever. The cantilever deflection is proportional to the force acting on the tip. This principle is applied in this lab course as well: Here, you are able to get to know the AFM and to image the surface of a CD and a DVD.

Topics:

Static AFM
Feedback loops
Interactions on the atomic scale
Lennard-Jones model

Please bring a USB drive to the lab course.

Theoretical foundations

The working principle

The setup of an AFM is shown schematically in figure . On the left-hand side of figure the actual AFM with sample, cantilever, deflection sensor and positioning system is shown. On the right-hand side of figure the data acquisition and the control for using the static AFM mode is shown.

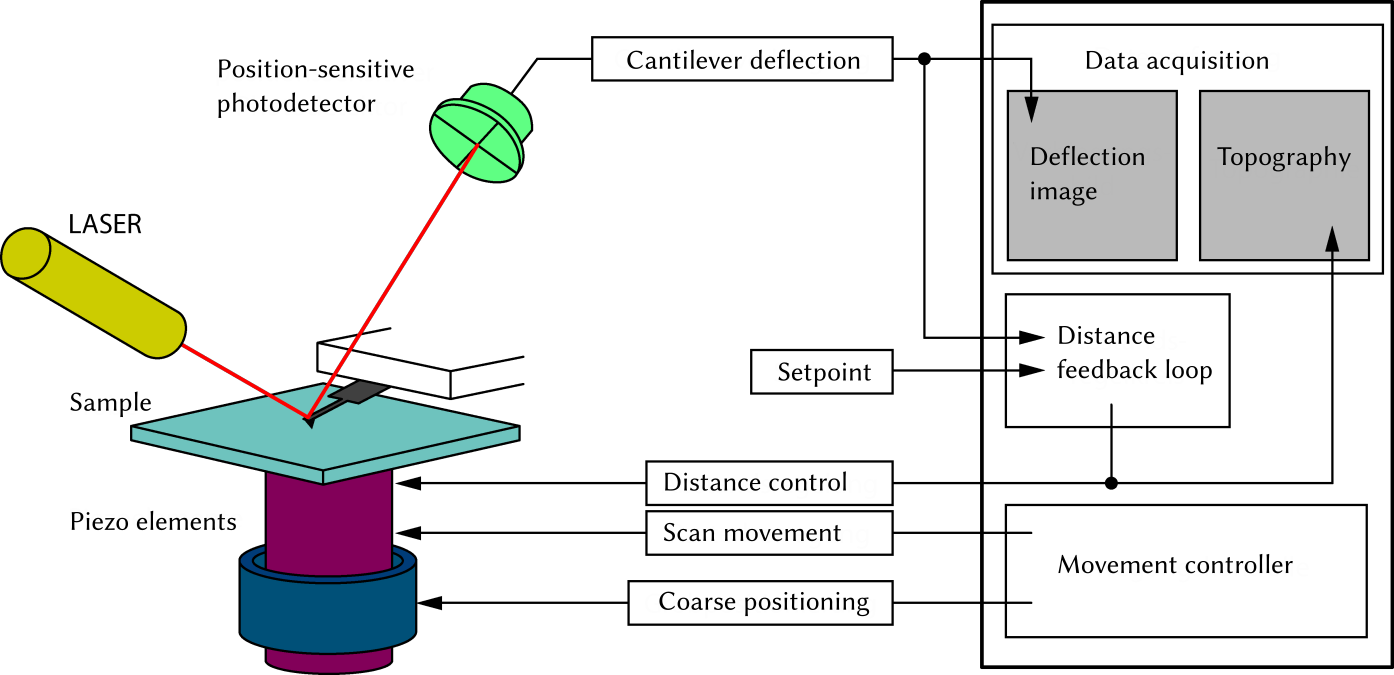
Schematic display of an AFM with data acquisition and control for using the static AFM mode.

Next, we shortly discuss the fundamental components necessary to detect the force acting on the measurement tip. We start with the Cantilever and its measurement tip attached to one end. The measurement tip is placed directly above the sample surface. A typical cantilever is shown in figure . To obtain an AFM image, the tip is scanned across the surface. As shown in figure the cantilever remains stationary and the sample is moved. The cantilever reacts to changes of the local sample properties (physical as well as chemical differences as well the topology) under the measurement tip with a change in the deflection, which is detected using a laser beam. The laser beam is focused on the cantilever back side, where it is reflected into a position-sensitive photo detector (PSPD). The PSPD is a four-segment photo diode, where the incoming light creates an electrical current in each segment. By (piecewise) summation of the signal of the individual segments the lateral and vertical deflection of the cantilever is determined.

Electron microscope image of a cantilever (left, scalebar 200 µm). The zoom (right, scalebar 20 µm) shows the free end of the cantilever with the tip. (Source: D. Steinigeweg, FB Biologie, Universität Osnabrück).

The scanning of the tip as well as the distance feedback is commonly realized using piezo elements. Depending on the device, either the sample can be moved, as shown in figure , or the cantilever. Piezo elements react to an electric field by a mechanical deformation. Depending on the applied voltage they expand or contract. This technique allows for precise mechanical movement on a subatomic length scale. An applied voltage of one volt typically causes a length change of around 10 nm. In AFM experiments, the relative distance between tip and sample is determined from the piezo extension $\vec r_\text p = (x_\text p, y_\text p, z_\text p)$ .

In static AFM, which is used in this lab course, only the static deflection $q_\text s$ of the cantilever is measured. This measurement results in a deflection image $q_\text s(x_\text p, y_\text p)$ of the sample. The cantilever deflection can be kept constant during the measurement by using a distance feedback loop. The distance feedback loop achieves this by changing the $z$ -position of the sample $z_\text p$ such, that the measured deflection corresponds to a predefined setpoint. If the force between tip and sample changes, the cantilever deflection will change accordingly. This change is detected using the PSPD signal from the reflected laser beam. The feedback loop reacts to this change of the deflection by moving the sample relative to the cantilever (either approaching or retracting), such that the deflection is restored to the previous value (corresponding to the predefined setpoint). Therefore, the $z$ -position of the sample follows a contour of equal cantilever deflection. On many samples, this contour of equal deflection $z_\text p (q_\text s = \text{const.})$ is similar to the surface topography. Therefore, the resulting image is called topography image $z_\text p(x_\text p, y_\text p)$ .

If the distance feedback loop is switch off, the sample scan be scanned with a large scan velocity. However, this method of constant height should only be used on flat samples, since the tip can easily be damaged by obstacles on the surface. Particularly with unknown samples it is very advisable to switch on the distance feedback loop to prevent tip damage by quickly retracting the tip upon an increase in deflection. However, the scan rate in the constant deflection mode is limited by the time it takes for the feedback to adjust the distance.

Since the cantilever is not only sensitive towards the force between tip and sample but also to external vibrations of the building, a good vibrational isolation of the AFM is crucial. Small vibrations of the building and even sounds (such as noise due to speaking in the lab) influence the measurement. The mechanical decoupling of the AFM from the building is often achieved by placing the AFM in a vibration-isolation table and a isolation housing.

Static AFM

The measurement electronic of the AFM always records the topography image $z_\text p(x_\text p , y_\text p)$ (image of the $z$ -piezo height) and the deflection image $q_\text{s} (x_\text p,y_\text p)$ (image of the static cantilever deflection). Both data channels together allow to determine the force between tip and sample as function of the distance. This relationship is explained in the following.

The force

As already mentioned above, the AFM is based on detecting the force acting between the sample surface and the tip. The force caused by the sample and acting on the tip $\vec F_\text{ts}(\vec r_\text{ts})$ is a function of distance $\vec r_\text{ts}=(x_\text{ts},y_\text{ts},z_\text{ts})$ between tip and sample. For conservative interactions the following relationship between force $\vec F_\text{ts}(\vec r_\text{ts})$ and potential energy $V_\text{ts}(\vec r_\text{ts})$ :

\vec F_\text{ts}(\vec r_\text{ts})=-\nabla V_\text{ts}(\vec r_\text{ts})=-\left(\frac{\partial V_\text{ts}(\vec r_\text{ts})}{\partial x_\text{ts}}, \frac{\partial V_\text{ts}(\vec r_\text{ts})}{\partial y_\text{ts}}, \frac{\partial V_\text{ts}(\vec r_\text{ts})}{\partial z_\text{ts}}\right)

In case of conservative interactions the force is the negative gradient of the potential energy. In this lab course, we assume for simplicity that the force only acts perpendicular to the sample surface: $\vec F_\text{ts}(\vec r_\text{ts}) = F_\text{ts} (\vec r_\text{ts})\vec e_\text z$ . Only the $z$ -direction (identified by $\vec e_\text{z}$ ) contributes to the normal component $F_\text{ts} (\vec r_\text{ts} )$ Using only this normal component, equation (1) simplifies to

\vec F_\text{ts}(\vec r_\text{ts})=-\left(0,0,\frac{\partial V_\text{ts}}{\partial z_\text{ts}(\vec r_\text{ts})}\right)\qquad\text{and}\qquad F_\text{ts}=-\frac{\partial V_\text{ts}(\vec r_\text{ts})}{\partial z_\text{ts}}

In the following we discuss first the dependence of the force with respect to the perpendicular distance $z_\text{ts}$ between tip and sample.

Besides the potential energy $V_\text{ts} (z_\text{ts})$ and the normal component of the force $F_\text{ts} (z_\text{ts})$ the force gradient $k_\text{ts}(z_\text{ts})$ can be determined. The force gradient quantifies the change of force relative to a change in distance:

k_\text{ts}(z_\text{ts})=\frac{\partial F_\text{ts}(\vec r_\text{ts})}{\partial z_\text{ts}}=-\frac{\partial^2 V_\text{ts}(\vec r_\text{ts})}{\partial z_\text{ts}^2}

Figure 3 shows the relationship between potential energy, force and force gradient. The dependence of the normal component from the perpendicular (normal) distance between tip and sample is often called force-distance curve $F_\text{ts}(z_\text{ts})$ .

Relationship between potential energy, force and force gradient (equation 3) of the tip-sample interaction. At the equilibrium distance

z_\text{eq}

(black vertical line) the force between tip and sample is zero and the potential energy is minimal:

V_\text{ts}(z_\text{ts} = z_\text{eq}) =-V_\text{eq}

Force-distance curve

During static AFM and in equilibrium, the sample and cantilever are stationary. As shown in figure 3, the force between tip and sample can be attractive or repulsive. With attractive interactions the cantilever bends towards the surface, repulsive interactions cause the cantilever to bend away from the surface. The static deflection results (1) from the interaction between sample and the tip on the free end of the cantilever and (2) from fixating the other end of the cantilever. In stable equilibrium the potential energy of the system consisting of cantilever and sample is minimal. The necessary condition for equilibrium therefore is: The force $F$ acting on the tip is zero. The restoring force, caused by the fixation of the cantilever end compensates the force that acts on the tip caused by the sample.

F = -k q_\text s + F_\text{ts} = 0 \Leftrightarrow F_\text{ts} = k q_\text s

Equation (4) means: If a force acts on the tip (caused by the sample) the cantilever reacts with a static deflection.

q_\text s = F_\text{ts} / k.

The linear relationship between the static deflection from the force $F_\text{ts}$ only is valid for small forces. Equation (5) is called Hooke’i law. The proportionality constant $k$ is the spring constant (and is a property of the cantilever. If the spring constant is known, the measured static deflection can be used to compute the force.

Equation (4) is a necessary condition for equilibrium (the potential energy is extremal). The sufficient condition (the extremum is a minimum) is:

\frac{\partial^2V}{\partial z_\text{ts}^2}= -\frac{\partial F}{\partial z_\text{ts}}= k-k_\text{ts}>0\Leftrightarrow k > k_\text{ts}.

If the condition $k>k_\text{ts}$ cannot be fulfilled, no stable equilibrium exists at the corresponding tip-sample distance. This part of the force-distance curve is, as shown in figure 4, not experimentally accessible. Instead, a the deflection changes very quickly when approaching the tip to the sample and when retracting the tip from the sample. The cantilever tip jumps whenever $k < k_\text{ts}$ is encountered. This effect makes it difficult to approach the tip successively (and carefully) to the sample and, in the worst case, might damage both sample and tip.

In the repulsive force region, the condition $k > 0 > k_\text{ts}$ causes equation (6) is always fulfilled. Therefore, static AFM is usually operated in the repulsive region. Here, the distance between tip and sample is rather small and does not change significantly upon approaching the fixed end of the cantilever. For this reason, static AFM is sometimes referred to as contact mode AFM. The term can be misleading, since static AFM could also be performed in the attractive region and because the distance between tip and sample in the repulsive region might be small, but never zero.

To achieve the largest sensitivity, it is useful to use soft cantilevers (small spring constant). In this case, a small change in force causes a large change of the deflection of the cantilever (see equation 5). However, small spring constants reduce the experimentally accessible range (equation 6).

The left panel shows the tip-sample force gradient

k_\text{ts}

as function of the tip-sample distance

z_\text{ts}

. The right panel shows the measured deflection

q_\text{s}

as function of the z-piezo distance

z_\text p

. In the simulation, the cantilever is first approached to the surface by reducing

z_p

(red points). After the approach, the cantilever is retracted from the surface (blue points). If

k_\text{ts}<k

the corresponding distance is accessible using static AFM. The region where

k_\text{ts} > k

cannot be experimentally accessed. A variation of the cantilever spring constant

k

restarts the simulation.

The distance between tip and sample is given as

z_\text{ts} = z_\text o + z_\text p + q_\text s .

However, the reference distance $z_\text{ts} = z_\text o$ if cantilever and sample are in their respective rest position ( $z_\text p = 0$ and $q_\text s = 0$ ), is usually not known. Therefore, in most cases only the relative distance $z_\text{ts} - z_0 = z_\text p + q_\text s$ is determined and discussed.

Using equations (5) and (7) the measured topography image $z_\text p(x_\text p, y_\text p)$ and the measured deflection image $q_\text s (x_\text p, y_\text p)$ can be used to determine a force image:

F_\text{ts}(z_\text{ts} = z_\text o + z_\text p + q_\text s) = k q_\text s.

Relevant interactions

Typical origins for the interaction between tip and sample are electrostatics (Coulomb force), the Van-der-Waals interaction as well as the exchange interaction (chemical bonds as well as Pauli repulsion). The electrostatics force and the Van-der-Waals force can be attractive or repulsive. They are usually of long range. Exchange interaction, in contrast, are forces with a short range and are either attractive (occupied bonding states) or repulsive (occupied anti-bonding states) Table 1 shows an overview over the interactions that are typically relevant for AFM as well as their distance-dependence. Additionally, the distance-dependence of the corresponding potential energy curves is states. This is possible, since the interactions discussed here are all conservative, which allows to use equation (1).

Interactions that are relevant for AFM with their distance dependence.
Interaction	Potential energy	Force
Electrostatic (for two point charges)	$\propto z_\text{ts}^{-1}$	$\propto z_\text{ts}^{-2}$
Van-der-Waals (for two rotating point dipoles)	$\propto z_\text{ts}^{-6}$	$\propto z_\text{ts}^{-7}$
Exchange interaction	Depends on the orbitals involved
Pauli repulsion	extremely short; often modeled as $\propto z_\text{ts}^{-12}$	$\propto z_\text{ts}^{-13}$

Electrostatics

Electrostatic interactions are described by the Coulomb law, which describes the force between two electrically charged particles. The force acting on a positively charged particle caused by a negatively (positively) charged particle is attractive (repulsive) and the force on a negatively charged particle caused by a negatively (positively) charged particle is repulsive (attractive): Equal charges repel each other, different charges attract each other.

Van-der-Waals force

For discussing the Van-der-Waals force it is useful to differentiate between the two partners of the interaction; there are three kinds: The interaction between permanent dipoles is called Keesom interaction. Here, the strength of the interaction is governed by the relative orientation of the dipoles and their dipole strength.

The Van-der-Waals force between a permanent dipole and an induced dipole is called Debye interaction. Here, the polarization plays a role, in addition to the dipole orientation and strength. Debye and Keesom interactions can be described using the Coulomb law and are sometimes assigned to electrostatic interactions. The third kind of Van-der-Waals interaction is fundamentally different to the first two. Here, the interaction between two induced dipoles is considered, which is sometimes called London dispersion force. The spontaneous fluctuations of the electron density distributions and the resulting spontaneously induced polarization between the two unpolar partners are of quantum mechanical origin and can only be modeled classically with approximations. All kinds of Van-der-Waals interactions can be modeled with a distance dependence of $1/z_\text{ts}^7$ between freely-rotating point-like interaction partners.

Exchange interaction and Pauli repulsion

At small distance between tip and sample the exchange interaction dominates. This interaction originates from the fact that electrons are fermions. If overlapping orbitals of the interaction partners are only partially occupied (mostly bonding states are occupied), the approach of the interaction partners causes the potential energy to decrease, i.e. an attraction. This chemical binding force is a quantum mechanical effect that depends on the properties (quantum state) of the involved electrons (orbitals). This makes it impossible to state a classical force law. If the overlapping orbitals are fully occupied (anti-bonding states are occupied) an approach causes an increase in potential energy, i.e. repulsion.

Since two fermions in the same quantum state cannot be at the same position, the Pauli repulsion becomes dominant at very small distances. This repulsion is as well an omnipresent quantum mechanical effect. In molecules, usually all energetically-favorable orbitals are occupied with a spin-up and spin-down state. An additional electron would therefore destabilize the system, which leads to repulsion. Pauli repulsion is present in every-day life: One does not fall through the floor, since the outer electrons of the molecules in your shoes and floor would need to enter higher-energy states if they were approached further. Due to practical considerations, the distance-dependence of this force is often modeled with $1/z_\text{ts}^{13}$ .

Lennard-Jones model

The interaction between tip and sample (figure 3) is often modeled using a Lennard-Jones model. This model states the potential energy $V_\text{LJ}(\vec r)$ of a system consisting of two neutral, chemically non-bonding interaction partners at distance $\vec r$ . If we transfer this model to tip and sample we obtain:

V_\text{LJ}=-V_\text{eq}\left[2 \left(\frac{z_\text{eq}}{z_\text{ts}}\right)^6 -\left(\frac{z_\text{eq}}{z_\text{ts}}\right)^{12} \right]

In this equation, $z_\text{eq}$ is the equilibrium distance, i.e., the distance at which the repulsive interactions compensate the attractive ones and the force is zero. The system is in equilibrium and the potential energy is minimal. $V_\text{LJ}(z_\text{ts} = z_\text{eq} ) = -V_\text{eq}$ .

For the display of the tip-sample interaction in figure (3) equation (9) was used, the equilibrium distance is shown as well (black vertical line).

As is obvious from figure 3, the Lennard-Jones model consists of an attractive and a repulsive contribution. The short-range Pauli repulsion is modeled using $\left(z_\text{eq} / z_\text{ts}\right)^{12}$ . The attractive part represents contributions from the Van-der-Waals attraction and dominates at larger distances. It is modeled by the term $-\left(z_\text{eq} / z_\text{ts} \right)^6$ . The Lennard-Jones model describes the potential energy as function of the distance under the assumption that the interaction partners are point-like. When considering actual geometries between tip and sample, this dependence changes. For example, a point-like tip and a flat sample can be described with an attractive contribution of $-(z_\text{eq} / z_\text{ts} )^3$ .

Visualization of the Lennard-Jones potential (top) with the resulting tip-sample force (middle) and the tip-sample force gradient (button) with adjustable potential depth

V_\text{eq}

and equilibrium distance

z_\text{eq}

Dynamic AFM

Besides the static AFM method with its constant-height and constant-deflection mode discussed above, there are a number of related AFM techniques, where the cantilever is oscillated. Therefore, the cantilever is never at rest, which lends those methods the name dynamic AFM.

In dynamic AFM, the deflection of the cantilever is not a static quantity. In the simplest case, the cantilever is excited by a sinusoidal force with a excitation force amplitude and an excitation frequency. As a consequence of the excitation, the cantilever oscillates with the excitation frequency. Besides the static excitation, in dynamic AFM also the amplitude of the dynamic cantilever excitation as well as the phase shift between the measured deflection relative to the excitation are measured. From the measured of all three quantities the force between tip and sample can be determined.

A variety of dynamic AFM modes exists, due to the fact that (multiple) feedback loops can be used to keep some of the measured quantities constant by adjusting others. Most-commonly used are AM and FM-AFM In AM-AFM, the excitation force amplitude and excitation frequency are constant and the change in amplitude and phase shift is measured. In FM-AFM, amplitude and phase shift are kept constant by two additional feedback loops by readjusting the excitation force and amplitude and the excitation frequency.

Static AFM is mostly performed in the repulsive regime (and therefore at small tip-sample distances). Soft samples (such as biological samples, cells, etc.) can be damaged during the measurement. Dynamic AFM is often used on such samples.

In dynamic AFM, a distance feedback loop that adjusts the $z$ position of the sample $z_\text p$ during the measurement is used as well. The setup is chosen such that some quantity (commonly the amplitude in AM-AFM and the excitation frequency in FM-AFM) is kept at a desired setpoint.

The distance feedback loop

In static AFM, the distance feedback loop changes the $z$ position of the sample $z_\text p$ (control variable) such that the static deflection (input variable) is equal to a predefined setpoint. The feedback loop compares the actual cantilever deflection $q_\text s^\text{actual}$ (actual value) with the desired value $q_\text s^\text{setpoint}$ (setpoint). If the actual value deviates from the setpoint, the feedback loop changes the control variable to eliminate the deviation $q_\text s^\text{setpoint}-q_\text s^\text{actual}$ .

The most important feedback loop is the integral (I) feedback loop. This circuit produces a control variable by integrating the deviation:

z_\text p(t) = K_\text I \int_0^t \left(q_\text s^\text{setpoint} - q_\text s^\text{actual}(t')\right) \mathrm dt'

Interactive visualization of a PI distance controller for static AFM. The upper panel shows the deflection

q

as function of piezo position in

x

direction (

x_\text p

). The setpoint

q_\text s^\text{setpoint}

can be adjusted.

The lower panel shows the adjusted piezo position $z_\text p$ (left ordinate) and the surface topography as the equilibrium distance $z_\text{eq}$ (right ordinate) for a simulated ridge in the center.

In the initial configuration, the controller is basically switched-off (very low gains). Try to increase first the I gain and then the P gain to keep the deflection constant and to evade the ridge.

Here, $K_\text I$ is a constant called I gain, which determines how large a deviation is weighted into the control output. An integral controller can eliminate the deviation completely after some time. The reaction of an integral controller depends solely in the choice of $K_\text I$ .

Usually, an integral controller is not used alone. The device used in the lab course uses a proportional-integral (PI) controller. The proportional controller generates a control variable that is proportional to the deviation:

z_\text p(t) = K_\text P \left(q_\text s^\text{setpoint} - q_\text s^\text{actual}(t)\right)

Here, $K_\text P$ is a constant called proportional gain, which weighs the contribution of the proportional controller.

A PI controller is a combination of an integral controller with a proportional controller (parallel circuit). The resulting control variable is the sum of equation the contributions in equation (10) and (11):

z_\text p(t) = K_\text I \int_0^t \left(q_\text s^\text{setpoint} - q_\text s^\text{actual}(t')\right) \mathrm dt' +K_\text P \left(q_\text s^\text{setpoint} - q_\text s^\text{actual}(t)\right)

The gains ( $K_\text I$ and $K_\text P$ ) are adjusted during the measurement such that the deviation is sufficiently small. The parameters cannot be chosen arbitrarily large since the feedback loop can start to oscillate and become chaotic/unstable, which could damage the tip and sample. If the gains are too small, the feedback loop cannot trace changes in the sample topography. This can lead to blurred contours of the surface and again to potential tip and sample damage. Depending on the sample and the tip velocity, the optimal settings are usually found empirically (by try-and-error).

Experimental setup

In this lab course, a MFP-3D AFM from Asylum Research is used. The experimental setup is shown in the following figure.

The AFM comes already connected to a computer. The insertion of the cantilever is done by the instructor. Do not exchange the cantilever by yourselves. The adjustment of the photo diode is done with instructions by the instructor. Align the laser onto the center of the free end of the cantilever. Next, adjust the PSPD such that the laser beam is centered on it as well.

To allow for both a high-resolution scan of the tip across the sample as well as a feasible exchange of the sample for which the cantilever has to be removed from the sample surface by several millimeter, the tip positioning is split into a coarse and a fine positioning system. The coarse adjustment is achieved with a setscrew at the front of the device. The fine adjustment is performed with piezo elements in the sub-nanometer to nanometer range.

Your instructor will guide you through the measurement software.

Instructions

Go to virtual lab course

Preliminary remarks

Make a note of all adjusted parameters (integral and proportional gain, setpoint, scan size, scan rate, scan direction, sample) for all datasets.
Make sure that you actually save the AFM images you wish to analyze.

Preparation

After the sample is inserted by the instructor and the laser is switched on, adjust the laser such that the maximum signal (Sum) is detected. Next, adjust the PSPD such that the detected deflection is zero (why?). Next, switch on the distance feedback loop and approach the cantilever to the sample until the deflection is equal to the setpoint and the piezo voltage (Z Voltage) is about 70 V (approx. half of the maximum range). What happens upon approach? Start the measurement.

Imaging a CD and a DVD

You will image various sample surfaces using static AFM.

Imaging the sample: Scan the first sample using the constant deflection mode and a scan size of $10 \cdot 10 \pu{μm2}$ .
Changing the feedback settings: Use a scan speed of 2 Hz. Change within an image the integral gain (5; 10; 20; 40; 80) with a switched-off proportional controller (P-Gain is 0). Next, change within one image the P gain (0,5; 1; 2; 4; 8) with a fixed I gain of your choosing. Discuss the difference in the image as well as the trace and retrace profile. What artifacts are visible? How do you determine that the feedback works well? Which parameters are the best?
Influence of the scan speed: Take the optimal feedback loop settings and record for various scan speeds (1 Hz; 2 Hz, 4 Hz, 8 Hz, 10 Hz) an image of size 10 x 10 μm² each. What is the effect of changing the scan speed on the obtained images?
Influence of external effects: Talk loudly/stomp on the floor/pound the table/touch the vibration table lightly. What is the effect on the measurement?
Changing the sample: Image the two prepared samples using two different scan ranges ( $20 \cdot 20\pu{μm2}$ and $5 \cdot 5 \pu{μm2}$ ), by selecting optimal values for the feedback loop and scan speed. What is the effect of the sample change on the image quality?

Change the values: Scan size, scan rate, integral gain and proportional Gain. Start the measurement with Do Scan and stop it with Stop. Using Frame Up and Frame Down you can restart an image during the scan. A fully recorded up or down image is automatically saved and the Base Suffix is incremented by one.

Analysis

Go to the analysis of the virtually-recorded data

Determine the width, length and height of the surface structures (including their uncertainty). Consider the used resolution, which can be determined from the pixel count (pixel count within each line, and line count) and the scan size.

On CDs and DVDs data is stored as a trace of height differences. An raised segment denotes a logical one, a normal (non-raised) segment a logical zero. What is the difference between DVD and CD? What is the influence of the geometry of the cantilever tip, the feedback loop (P and I gain) and external influences on the measurement?

For the analysis of your AFM images you can use the software Gwyddion. The software is available on the measurement computer in the lab and can be downloaded from https://www.gwyddion.net. The software is open-source and available for most operating systems. Documentation is available on the website.

After opening a file using File → Open, you can use the data browser (in the menu Meta → Data Browser) to select your image channel of choice. The most important operations and tools are available from the main window.

Adjustment of the color scale in Gwyddion.

The first two functions allows to measure the size and angle of structures in the image.

After selecting the line profile tool you can extract individual profiles and, additionally, determine distances within the profile.

Under File → Save As … the edited images can be saved. To export data from graphs or tables you can find the corresponding function under Graph → Export As ….

Should you have further questions regarding Gwyddion you can look up the online manual or ask your supervisor.

Preparation, analysis and lab report

Bring a USB drive to store your AFM data. For preparing for the preliminary test, you should read this script and be able to answer the following questions regarding the theory and setup of AFM.

Enumerate the forces that are relevant in AFM and their distance dependence. What is the relationship between force, potential energy and force gradient?
What AFM techniques are available? What signals are measured?
What is the setup of static AFM? What are the advantages and disadvantages of using a distance feedback loop?
How does a feedback loop work?
What images are recorded in the static AFM mode? Is it useful if the cantilever is particularly hard or soft?

After finishing the lab course, write a report and send it to your instructor digitally (via email).

Write your report according to the Kompendium Grundpraktikum Physikalische Chemie. Answer all questions raised in chapters 3 and 4 and make sure the following parts are included: Short theory, setup, execution, analysis, discussion, summary, appendix. Attach a copy of all notes made during the lab course in the appendix.

Literature

Binnig, G., Quate, C.F. and Gerber, Ch., Atomic Force Microscope, Phys. Rev. Lett. 56, 930 (1986)
Kaupp: Atomic Force Microscopy, Scanning Nearfield Optical Microscopy and Nanoscratching. Springer-Verlag. 2006
Braga, Ricci: Atomic Force Microscopy. Humana Press. 2004
Foster, Hofer: Scanning Probe Microscopy. Springer Science+Business Media. 2006