まず、積分を計算することは面積を求めることに他ならない、ということを思い出しておこう。 数値積分にはいろいろな方法があるが、ここでは台形公式を取り上げる。
台形公式
例えば、 \[ \int_{0}^{3} f(x) \mathrm{d} x \] \[ f(x) = x^3 - 5 x^2 + 7 x + 1 \] を求めたいとする。これは下の図で薄い青で塗られた部分の面積である。
このとき、区間をさらに細かい区間に分け、それぞれを台形で近似する (曲線を折れ線で近似していると見ることもできる)。 いくつの区間に分けるかは、求めたい精度による (がここでは立ち入らない)。
以下でスライダーをいじってみて欲しい。 分割数 $n = 3, 4, 5$ あたりの様子を見ると何をやっているか分かりやすいだろう。 そして $n$ をどんどん大きくしていくと、求めたい面積にどんどん近づいていくことが分かるだろう。
| $S$ | $9.75$ |
|---|---|
| $S'$ | |
| Error $/ \%$ |
ここで、 $S$ は真の値、 $S'$ は台形公式で求めた値、 Error は $(S' - S) / S$ (をパーセント表示したもの) である。
台形公式の場合は、
-
各区間が一定でなくても良い
という特徴がある。
区間が一定の場合
各記号を次図のように定義する。
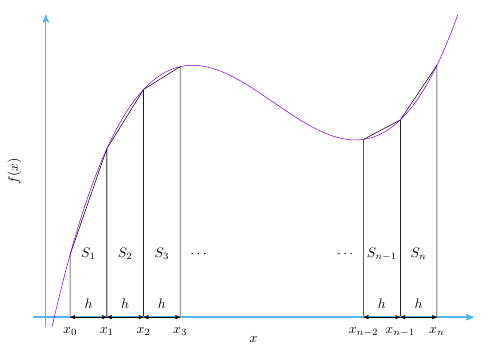
考え方
まずは簡単な区間が一定の場合で考えてみよう。 各区間の長さを $h$ とする。
すると、
-
最初の台形の面積 $S_1$ は、 $$ S_1 = \frac{\left(f(x_0) + f(x_1)\right) h}{2} $$
-
次の台形の面積 $S_2$ は、 $$ S_2 = \frac{\left(f(x_1) + f(x_2)\right) h}{2} $$
-
…
-
最後の台形の面積 $S_n$ は、 $$ S_n = \frac{\left(f(x_{n-1}) + f(x_n)\right) h}{2} $$
となる。
あとはこれらを足せば良いだけである。 すなわち、求める積分の近似値 $S'$ は
$$\begin{align*} S' & = \frac{\left(f(x_0) + f(x_1)\right) h}{2} + \frac{\left(f(x_1) + f(x_2)\right) h}{2} + \cdots + \frac{\left(f(x_{n-1}) + f(x_n)\right) h}{2} \end{align*}$$
となる。 これをプログラムとして書けばよい。
簡略化
と言いたいところだが、ちょっとだけ立ち止まってよく考えてみよう。
まず一般論として、
このことを踏まえて、上の式を見直してみよう。
-
$S_1$ と $S_2$ を良く見て欲しい。 どちらにも、$\frac{f(x_1) h}{2}$ が含まれている。 半分にしているものを二つ足しているのだから、そもそも 2 で割る必要がない。
-
同様に、$f(x_1)$ を二回計算しているが、これも一回で済ませられる。
-
また、全ての $S_i \; (i = 1, 2, ..., n)$ には $h$ が掛けられているが、毎回掛け算せずとも最後に一回だけ掛ければ良い。
一般的には $f(x)$ の計算には非常に時間がかかる (時間がかからないような場合は、そもそも数値積分するまでもなく計算できることがほとんど)。 例えば $f(x) = \mathrm{e}^{-x^2}$ だったとすると、$x^2$ の計算に時間がかかり、$\exp$ の計算でさらに時間がかかる。 従って $f(x)$ の計算回数もできるだけ減らすべきである。
結局のところ、上の式は次のように書きかえることができる。 \[ S' = \left( \frac{f(x_0)}{2} + f(x_1) + f(x_2) + ... + f(x_{n-1}) + \frac{f(x_n)}{2} \right) h \] あるいは、さらにこだわれば、 \[ S' = \left( \frac{f(x_0) + f(x_n)}{2} + f(x_1) + f(x_2) + ... + f(x_{n-1}) \right) h \] となる。
掛け算の回数が $n$ 回から 1 回 (!) になっており、割り算の回数も $n$ 回から 2 ないし 1 回になっている。 また、最初の式では $f(x)$ は $2n$ 回出てきているが、後の式では $n + 1$ 回でほぼ半分になっている。 これらは数学的には全く同一だが、コンピューターでの計算と考えると異なる。
小まとめ
(積分に限らず) ある計算をさせるプログラムを書く手順は、概ね、
-
計算方法の原理を考える
-
その為に必要な計算式を導出する
-
その式を検討し、簡略化等の余地がないか考える
-
プログラムを書く
となる。
このことから分かるのは、プログラムを書くよりも、 その前段階 (準備) の方が多く、重要である ということである。 プログラムを書く前の準備を適当にやってしまうと、とてつもなく遅いプログラムになったり、誤差が大きくなったりするおそれがある。
もちろん特に最初のうちはとりあえず手を動かしてみるというのも悪くない。 ただしその場合も「あとで検討しなおすことが必要で、その際プログラムが大きく変更になる可能性が高い」ことを認識しておくことが重要である。
区間が一定ではない場合
考え方は一定の場合とほとんど同じである。 $h$ が各区間 $h_1 = x_1 - x_0$, … に置きかわるだけである。
$$\begin{align*} S' = & \frac{\left(f(x_0) + f(x_1)\right) h_1}{2} + \frac{\left(f(x_1) + f(x_2)\right) h_2}{2} + \cdots + \frac{\left(f(x_{n-1}) + f(x_n)\right) h_{n}}{2} \end{align*}$$
残念ながらこの場合はあまり簡略化できない。
$$\begin{align*} S' = & \frac{1}{2}\left( f(x_0) h_1 + f(x_1) (h_1 + h_2) + \cdots + f(x_{n-1}) (h_{n-1} + h_{n}) + f(x_n) h_{n} \right) \\ = & \frac{1}{2}\left( f(x_0) (x_1 - x_0) + f(x_1) (x_2 - x_0) + \cdots + f(x_{n-1}) (x_{n} - x_{n-2}) + f(x_n) (x_n - x_{n-1}) \right) \end{align*}$$
台形公式以外の方法
数値積分の方法として台形公式以外の代表的なものに、合成シンプソン公式がある。 興味があれば調べてみて欲しい。
練習 1
では、実際に台形公式による数値積分のプログラムを書いてみよう。
ここではまず $f(x) = x$ の面積を求めてみることにしよう。
-
$f(x) = x$ のグラフを描け (紙と鉛筆で)
-
$f(x) = x$ を求める関数を (JavaScript で) 書き、$x = 0, 1, 2$ での値を表示させよ。 表示された結果が正しい値であることを確認せよ。
具体的には以下のような感じになるであろう。 関数名等は変更してもよい。
function f(x) { // ここを書く return ...; } console.log(f(0)); console.log(f(1)); console.log(f(2)); -
次の値を (紙と鉛筆で) 計算せよ
$$\begin{align} \int_0^1 f(x) \,\mathrm{d}x \\ \int_1^2 f(x) \,\mathrm{d}x \end{align}$$
-
数値積分を求める関数を書け。 引数として、積分区間の下限 $x_\mathrm{l}$, 積分区間の上限 $x_\mathrm{u}$, 分割数 $n$ を取るものとせよ。 例えば:
function integral(xl, xu, n) { // ここを書く return ...; }関数名、変数名、引数の順番は変えてもよい。
プログラムを書いていると、いくつか悩むところがあるかもしれないが、まずはいろいろと試してみよう。 この後にヒントが書かれているが、まずは見ずにチャレンジしてみて欲しい。 -
この関数を使って、以下の組み合わせで実行してみよ。 この場合、いずれの場合も厳密に正しい結果が得られるはずである (なぜか? 考えてみよ)。 正しい結果が得られたか確認せよ。
-
$(x_\mathrm{l}, x_\mathrm{u}, n) = (0, 1, 1)$
-
$(x_\mathrm{l}, x_\mathrm{u}, n) = (0, 1, 2)$
-
$(x_\mathrm{l}, x_\mathrm{u}, n) = (0, 1, 16)$
-
$(x_\mathrm{l}, x_\mathrm{u}, n) = (0, 1, 1000)$
-
$(x_\mathrm{l}, x_\mathrm{u}, n) = (1, 2, 1)$
-
$(x_\mathrm{l}, x_\mathrm{u}, n) = (1, 2, 2)$
-
$(x_\mathrm{l}, x_\mathrm{u}, n) = (1, 2, 16)$
-
$(x_\mathrm{l}, x_\mathrm{u}, n) = (1, 2, 1000)$
(つまり、積分区間 [0, 1], [1, 2] それぞれに対し分割数 1, 2, 16 及び 1000 での数値積分)
-
ヒント: $x_i$ の求め方
もしかすると、$x_i$ の求め方で悩んだかもしれない。
方法 1
最も素朴な方法は、最初に $h$ を求めておいて、それを $x_0$ ($= x_\mathrm{l}$) に足していく方法である。
let x = xl;
let h = (xu - xl) / n;
for ( ... ) {
...
x += h;
...
}
しかし $h$ の値は (コンピューター内部では) 誤差を含みうるので、この方法では誤差が蓄積していく可能性がある (数値計算で注意すべきこと: 誤差入門 も参照せよ)。
方法 2
もう一つの方法は、
$$x_i = x_\mathrm{l} + \frac{\left(x_\mathrm{u} - x_\mathrm{l}\right) \times i}{n}$$ と書けることから、これを毎回計算する方法である。 こちらは $h$ の誤差に起因する誤差を抑えることができるが、掛け算・割り算の回数が増えてしまう。
比較
これらの方法を誤差の観点から比較してみよう。 いずれの方法でも数学的には同一の値が得られるはずなのに、なぜ違いが出る (場合がある) のか疑問に思うかもしれない。 一言で言うと、「コンピューターは無限桁を扱えない」ことに起因する。
分かりやすくするために十進数で考えてみよう。 区間 [0, 1] を 3分割し、その間の点を求めたいとする。 ここでは有効数字 3 桁としよう。
第一の方法では、$h = (1 - 0) / 3 = 1 / 3 = 0.333$ となる。 従って $x_i$ は次のようになる: $$\begin{align*} x_0 &= 0 \\ x_1 &= x_0 + h = 0.333 \\ x_2 &= x_1 + h = 0.666 \\ x_3 &= x_2 + h = 0.999 \end{align*}$$ $x_3 = 1$ であるはずなのだが、$h$ の誤差に起因した誤差が生じている。
第二の方法では、 $$\begin{align*} x_0 &= 0 \\ x_1 &= x_0 + \frac{(1 - 0) \times 1}{3} = 0.333 \\ x_2 &= x_0 + \frac{(1 - 0) \times 2}{3} = 0.667 \\ x_3 &= x_0 + \frac{(1 - 0) \times 3}{3} = 1 \end{align*}$$ となり、第一の方法より誤差が抑えられていることが分かる。 (第二の方法でも、$x_1$, $x_2$ は厳密な値ではないことに注意しよう。実際にはこれらは無限小数である。)
ただし、第一の方法で必ず誤差が発生する訳ではない。 $h$ が誤差を含まなければ (例えば十進数の場合であれば $h = 0.2$ などの場合)、それによる誤差は発生しない。
-
$f(x) = x^2$ のグラフを描け
-
次の値を (紙と鉛筆で) 計算せよ
$$\begin{align} \int_0^1 f(x) \,\mathrm{d}x \\ \int_1^2 f(x) \,\mathrm{d}x \end{align}$$
-
前練習問題で作成したプログラムの
f(x)の部分のみを変更し、実行せよ。 どのような値が得られ、なぜそのような結果になったか検討せよ。 -
余裕があれば、$x_i$ を求める方法として上記の二つの方法それぞれでプログラムを書き、結果を比較してみよ。
検算方法 (その 1)
プログラムの間違いを修正するのは、プログラムを書くより大変な作業である。 特に大規模なプログラムの場合、後になればなるほど間違いを見つけるのが困難になる。 従って、最初のうちに間違いの発生しそうなところを事前に察知し、そこに間違いがないかどうか確認することで、 早いうちに徹底的に間違いを排除しておくことが重要である。 残念ながらそのような「間違いの発生しそうなところ」を察知するには経験が必要になることが多い。 (たくさん間違ったことがあるプログラマーは、そのような勘を働かせやすい。今のうちにたくさん間違っておこう!)
ここでは、いくつか典型的な間違いやすいポイントを見てみよう。 基本的には「例外的」あるいは「特別」な部分に間違いが発生しやすいので、そのようなポイントでうまく動いているか確認することが重要である。
最初の練習問題では、$f(x) = x$ に対して、
-
$(x_\mathrm{l}, x_\mathrm{u}, n) = (0, 1, 1)$
-
$(x_\mathrm{l}, x_\mathrm{u}, n) = (0, 1, 2)$
-
$(x_\mathrm{l}, x_\mathrm{u}, n) = (0, 1, 16)$
-
$(x_\mathrm{l}, x_\mathrm{u}, n) = (0, 1, 1000)$
-
$(x_\mathrm{l}, x_\mathrm{u}, n) = (1, 2, 1)$
-
$(x_\mathrm{l}, x_\mathrm{u}, n) = (1, 2, 2)$
-
$(x_\mathrm{l}, x_\mathrm{u}, n) = (1, 2, 16)$
-
$(x_\mathrm{l}, x_\mathrm{u}, n) = (1, 2, 1000)$
で検算をした。 このような値を選んだのにはそれなりに訳がある。 まず関数を $f(x) = x$ としたのは、計算が簡単だからである。 最初に区間 [0, 1] を選んだのも、検算が簡単だからである。 ここで間違った答が出ている場合は、根本的にプログラムが間違っている可能性が高い。 加えて [1, 2] を選んだのは、$x_\mathrm{l}$ の扱いを間違っていないか確認するためである。 これらは共に区間の長さが 1 であるが、そうでない場合 (例えば区間 [1, 3] や [1, 2.1] など) も確認するとさらに良い。
分割数については、最初に $n = 1$ の場合を確認した。 というのは、どのようなプログラムを書いたかにもよるが、素直に、
let area = f(xl) / 2;
for (let i = 1; i < n; i++) {
x = ...;
area += f(x);
}
area += f(xu) / 2;
...
のようなプログラムを書いたとしよう。
このとき、$n = 1$ であったら for ループが実行されない (実行されないのが正しい動作である)。
このような「特別な場合」は間違いが入りやすい場所である。
$n = 2$ は for ループが一回だけ実行される場合である。
また $n = 16$ は (この場合、具体的な数字はそれほど重要ではない) より一般的な場合である。
さらに、$n = 1000$ も試した。これは 16 がコンピューターにとって「特別」な数字 ($2^4$) であるので1、そうではない数字を選んだ。
また、少し大きめの数字にすることで、極端に時間がかからないかどうかの確認も兼ねている。
(使用しているコンピューターや計算させたい関数にもよるが、分割数 $n = 1000$ 程度の計算はほとんどの場合一瞬で終わるだろう。)
また、練習問題 2 での $f(x) = x^2$ は $n$ によって得られる結果が異なる例である。
繰り返しになるが、たくさん間違えるのは、今後のために良い経験である。 間違えたときは、何をどのように間違えたか、ゆっくり考えてみよう。 こうした間違いの経験を積み重ねることは、よりよいプログラムを書けるようになるために必要なステップである。
練習 2
では、より実用的な問題を解いてみよう。
と言っても、上の問題でのプログラムがきちんと書けていれば、求める関数の部分以外はほとんど変更の必要は無いはずである (もし大きな変更が必要であった場合は、なぜそのようになったか分析しよう)。
-
上式では積分区間に $-\infty$ があるので、そのままでは数値積分できない。そのため、まず $$ \int_{-\infty}^0 \frac{1}{\sqrt{2\pi}} \exp\left(-\frac{x^2}{2}\right) \mathrm{d}x $$ (積分区間に注目せよ) を考える。 この式の値を答えよ。 またそれは何故か。
(ヒント: 計算せずに解答できる)
-
$f(x) = \exp\left(- \frac{x^2}{2}\right)$ を求める関数を書け。また $x=0, 1/2, 1$ での $f(x)$ の値を表示させよ。
-
この関数を用いて、台形公式により積分を求めよ。 $a$ 及び $n$ の値を変えて、積分値を求めてみよ。また真の値と比較せよ。
真の値は例えば Keisan Online Calculator > Standard normal distribution Calculator (CASIO COMPUTER CO., LTD.) で計算することができる。
let wavelength = [ 320.0, 320.2, 320.4, 320.6, 320.8, 321.0, 321.2, 321.4,
321.6, 321.8, 322.0, 322.2, 322.4, 322.6, 322.8, 323.0,
323.2, 323.4, 323.6, 323.8, 324.0, 324.2, 324.4, 324.6,
324.8, 325.0, 325.2, 325.4, 325.6, 325.8, 326.0, 326.2,
326.4, 326.6, 326.8, 327.0, 327.2, 327.4, 327.6, 327.8,
328.0, 328.2, 328.4, 328.6, 328.8, 329.0, 329.2, 329.4,
329.6, 329.8, 330.0 ];
let intensity = [ 6.821, 5.984, 6.159, 6.139, 5.903, 6.048, 6.008, 5.823,
5.376, 5.701, 5.395, 5.225, 5.220, 4.676, 5.028, 4.680,
4.692, 4.355, 4.969, 5.486, 7.238, 8.392, 9.946, 11.86,
13.87, 15.12, 16.22, 16.63, 16.56, 15.96, 13.95, 11.68,
10.04, 7.996, 6.554, 5.097, 4.336, 4.100, 3.695, 3.012,
3.058, 2.864, 2.588, 2.428, 1.931, 1.933, 2.071, 2.053,
1.476, 1.993, 2.058 ];
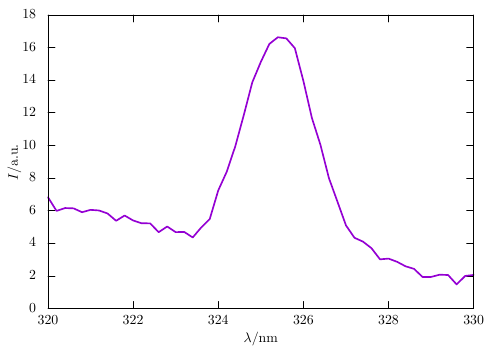
検算方法 (その 2)
以下は数値計算に限らず一般的に言えることであるので、ぜひしっかり理解して欲しい。
さて、最後の練習問題においては、最初のものと違って検算がしにくいので、 プログラムに間違いがないかを確認するのがやや難しい。
このような場合、
-
簡単なデーターで試してみる
-
大雑把な値を見積り、比較する
などが有効である。
簡単なデーターでの確認
例えば、
let wavelength = [ 1, 2 ];
let intensity = [ 1, 1 ];
let wavelength = [ 1, 2, 3 ];
let intensity = [ 1, 1, 2 ];
など、簡単に確認できるもの (手計算もプログラミングも楽なもの) を選んで結果を確認するとよいだろう。
また、 console.log() を使って、使っているデーターや中間結果を表示させるのも良いだろう。
ただし、簡単すぎると「たまたま」正しい結果がでる場合もありうるので、いくつかのパターンで試してみるのが良い。
上の例では一つ目は長方形の場合、二つめはそれに加えて台形になる場合になるようにしている。 この他に、値が負になる場合、三角形になる場合 (intensity が 0 のものを含む場合) なども確認するとより良い。
大雑把な見積り
また、上の練習問題では、例えば次のように見積ることができる。
-
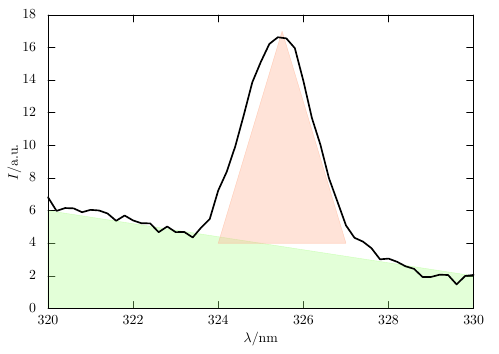
グラフの下の部分は大雑把に台形 (下図の緑の部分) に見えるから、この面積は $(6 + 2) \times (330 - 320) / 2 = 40$ くらいであろう。
-
「山」の部分は非常にざっくり見て三角形 (下図の赤の部分) とみなせるであろう。 するとその面積は $(327 - 324) \times (17 - 4) / 2 = 19.5$ くらいであろう。
-
これらの和は 59.5 であるから、だいたい 60 から極端に外れていない値であれば、おそらく正しく計算できているであろうと思うことができる。 もし 300 とか 10 とかの極端に違う値が出ていたら、どこかで間違っている可能性が高い。
意外に思うかもしれないが、このような単純な見積りは、実際の場面で非常に有効なことが多い。
その他の注意事項
境界に注意
繰り返し (ループ)でも述べたが、
一般に、ループ (特に for) ではループ条件が正しいかどうかを慎重に検討すべきである。
もし、上の練習問題の結果が NaN (Not a number の意味である) などになっていれば、ループ条件が間違っている可能性がある。
単位
以上の議論では単位については省略してきたが、この姿勢は正しくない。
通常、数値計算では数値のみを求め、単位に関しては関知しない。 そのため、単位は (プログラムの外で) 人間が補完してやる必要がある。
実は、区間の長さ 1 と 分割数 $2^4$ の組み合わせは、二進数において $h$ の誤差がない組み合わせの一つである。